Re-posted from: http://www.stochasticlifestyle.com/julia-ifem2/
This is the second post looking at building a finite element method solver in Julia. The first post was about mesh generation and language bindings. In this post we are going to focus on performance. We start with the command from the previous post:
node,elem = squaremesh([0 1 0 1],.01)
which generates an array elem where each row holds the reference indices to the 3 points which form a triangle (element). The actual locations of these points are in the array node, and so node(1) gives the points in the (x,y)-plane for the 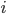 th point. What the call is saying is that these are generated for the unit square with mesh-size .01, meaning we have 10201 triangles.
th point. What the call is saying is that these are generated for the unit square with mesh-size .01, meaning we have 10201 triangles.
The approach to building the stiffness matrix for the Poisson equation is described here. The general idea is that span our vector space by a basis of hat functions  , and the so the stiffness matrix is found by the inner product (integral) between these basis functions. This translates to solving for the area of the triangles where two hat functions overlap, which we can do exactly since we chose the basis to be sufficiently nice. However, since the hat functions are zero except in a small range, most of these inner products are zero, meaning the resulting stiffness matrix is sparse. Our goal is to produce this sparse matrix as efficiently as possible. Lets get to it!
, and the so the stiffness matrix is found by the inner product (integral) between these basis functions. This translates to solving for the area of the triangles where two hat functions overlap, which we can do exactly since we chose the basis to be sufficiently nice. However, since the hat functions are zero except in a small range, most of these inner products are zero, meaning the resulting stiffness matrix is sparse. Our goal is to produce this sparse matrix as efficiently as possible. Lets get to it!
Building the Julia Version: Local Stiffness
The first function we need is titled localStiffness, which evaluates the inner product to give the “stiffness for one triangle”. In MATLAB the code is of the form:
function [At,area] = localstiffness(p) At = zeros(3,3); B = [p(1,:)-p(3,:); p(2,:)-p(3,:)]; G = [[1,0]',[0,1]',[-1,-1]']; area = 0.5*abs(det(B)); for i = 1:3 for j = 1:3 At(i,j) = area*((BG(:,i))'*(BG(:,j))); end end end
It takes in a vector p of three points, solves for the area at the reference triangle, and transforms the area appropriately to give the stiffness for the triangle defined by the points of p. I want to make a few points about this code. First of all, it employs a “trick” for solving for the dot product. That is, it uses the transposed vector times another vector. I quote trick because to a mathematician, this is simply the definition of the dot product, and so it only seems natural to use it like this in MATLAB. However, two things to point out. First of all, in Julia, such an operation does not return a scalar, but a one dimensional vector. This in some cases will give unexpected errors, so it should be avoided. Not only that, but it is also inefficient. In both MATLAB and Julia, matrices are stored column-wise, that is they are stored as a array of pointers where the pointers go to an array of columns. Thus to access a row matrix, both MATLAB and Julia would have to access the pointer and then go to the array at which it points (a size 1 array), and take the value there. Notice this is an extra step. Therefore it’s more efficient to keep the vectors column-wise. (In reality, the vectors here are so small that it won’t make a difference, but this justifies that the change we will do for the Julia code in a performance-sense).
Two other small changes were made to this code. For one, Julia throws an error at the definition of G since it cannot read the transpose calls inside of an array declaration. This is easily fixed by simply transposing after the creation instead. Lastly, we change the pre-allocation of At from zeros to Julia’s general constructor. This is slightly more performant since it will allocate the space without doing an initial re-write step, saving the time it would take to loop through and set each value to zero. The result is the following:
function localstiffness(p) At = Array{Float64}(3,3); B = [p[1,:]-p[3,:]; p[2,:]-p[3,:]]; G = [1 0 ; 0 1 ; -1 -1]'; area = 0.5*abs(det(B)); for i = 1:3 for j = 1:3 At[i,j] = area*dot(BG[:,i],BG[:,j]); end end return(At,area) end
which is ever so slightly more efficient, but in reality the same and just tweaked for the quirks.
Building the Julia Version: Matrix Assembly
Now we need to loop through each triangle and sum up the inner product between each pair of basis functions over each triangle. The intuitive code is:
function assemblingstandard(node,elem) N=size(node,1); NT=size(elem,1); A=zeros(N,N); for t=1:NT At,=localstiffness(node[vec(elem[t,:]),:]); for i=1:3 @simd for j=1:3 @inbounds A[elem[t,i],elem[t,j]]=A[elem[t,i],elem[t,j]]+At[i,j]; end end end return(A) end
I discussed previously the use of macros to speed up code without changing its style. The main problem that had to addressed in porting the code to Julia was that Julia will only take a vector for array referencing when the colon operator is used. Therefore since elem[t,:] returns a 1×3 Matrix of indices for the points associated with triangle  , once again a 1×3 Matrix is not an array in Julia so it throws an error. This is easy to fix by wrapping it in the vec() command, which others have tested to be the fastest method for conversion, and will actually do some fanciness in the background in order to not have to copy the array. This means that the cost of using vec is so small that I will use it liberally as a fix in these cases. Notice that within the loop vec is not required to reference A. This is because the issue only occurs when the colon operator is present.
, once again a 1×3 Matrix is not an array in Julia so it throws an error. This is easy to fix by wrapping it in the vec() command, which others have tested to be the fastest method for conversion, and will actually do some fanciness in the background in order to not have to copy the array. This means that the cost of using vec is so small that I will use it liberally as a fix in these cases. Notice that within the loop vec is not required to reference A. This is because the issue only occurs when the colon operator is present.
However, since At is usually zero, we can improve this a lot by instead generating vectors to build a sparse matrix. What we will instead do is save the (i,j) pairs where the value should be stored, and the value, and use the sparse command to reduce. The sparse command will automatically add together the values from repeated (i,j) indices, effectively performing the update we had before. This gives us the code:
function assemblingsparse(node,elem) N = size(node,1); NT = size(elem,1); i = Array{Int64}(NT,3,3); j = Array{Int64}(NT,3,3); s = zeros(NT,3,3); index = 0; for t = 1:NT At, = localstiffness(node[vec(elem[t,:]),:]); for ti = 1:3, tj = 1:3 i[t,ti,tj] = elem[t,ti]; j[t,ti,tj] = elem[t,tj]; s[t,ti,tj] = At[ti,tj]; end end return(sparse(vec(i), vec(j), vec(s))); end
Notice here that vec() needed to be used to build the sparse matrix because the easiest way to index within the loop was to use a 3-dimensional array and then flatten it via vec(). Notice a neat Julia trick where you can define multiple for loops in one line: “for ti = 1:3, tj = 1:3” is two loops and works as you’d expect. With some extra work we can get rid of the loop over the triangles by performing the calculations from localstiffness vector-wise, which gives us the vectorized form:
function assembling(node,elem) N = size(node,1); NT = size(elem,1); ii = Vector{Int64}(9*NT); jj = Vector{Int64}(9*NT); sA = Vector{Float64}(9*NT); ve = Array{Float64}(NT,2,3) ve[:,:,3] = node[vec(elem[:,2]),:]-node[vec(elem[:,1]),:]; ve[:,:,1] = node[vec(elem[:,3]),:]-node[vec(elem[:,2]),:]; ve[:,:,2] = node[vec(elem[:,1]),:]-node[vec(elem[:,3]),:]; area = 0.5*abs(-ve[:,1,3].*ve[:,2,2]+ve[:,2,3].*ve[:,1,2]); index = 0; for i = 1:3, j = 1:3 @inbounds begin ii[index+1:index+NT] = elem[:,i]; jj[index+1:index+NT] = elem[:,j]; sA[index+1:index+NT] = sum(ve[:,:,i].* ve[:,:,j],2) ./(4*area); # Replacing dot(ve[:,:,i],ve[:,:,j],2) index = index + NT; end end return(sparse(ii,jj,sA)); end
Here I note that Julia’s dot product will not act on matrices, only vectors. In order to do the row-wise dot product like we would do in MATLAB, we can simply use .* and sum the results in each row.
Dispelling a Myth: Vectorized Julia Rocks!
The most common complaint about Julia that people tend to have is that, in many cases, the code which gets the most performance is the de-vectorized code. “But the vectorized code can be so beautiful! Why would I want to change that?”. This myth seems to come from the alpha days or really bad tests, but it doesn’t seem to die. Instead, what I wish to show here is that vectorized code is also faster in Julia. First we run some basic timings:
@time assemblingstandard(node,elem); @time assemblingsparse(node,elem); @time assembling(node,elem); 0.538606 seconds (2.52 M allocations: 924.214 MB, 12.79% gc time) 0.322044 seconds (2.52 M allocations: 137.714 MB, 21.53% gc time) 0.015182 seconds (775 allocations: 28.650 MB, 16.97% gc time)
These timings pretty stability show this pattern. All of the methods were tried with parallelization and simd options with either no speedup or it being detrimental given the problem size. What this shows is that, out of the intuitive forms for solving these equations, the vectorized form was by far the fastest. The reason is that this is a highly vectorizable problem, whereas I discussed before the limitations that can cause vectorization to lose to devectorization.
But how does this fare against MATLAB? The “same” code was run in MATLAB (this is from iFEM, an optimized library Professor Long Chen) which gives the results:
tic; assemblingstandard(node,elem); toc; tic; assemblingsparse(node,elem); toc; tic; assembling(node,elem); toc; Elapsed time is 0.874919 seconds. Elapsed time is 0.698763 seconds. Elapsed time is 0.020453 seconds.
To ensure the time difference between the vectorized versions, we had both problems solve it in a loop:
@time for i = 1:1000 assembling(node,elem); end 9.312876 seconds (821.25 k allocations: 27.980 GB, 21.32% gc time)
vs MATLAB:
tic; for i=1:1000 assembling(node,elem); end toc; Elapsed time is 19.221982 seconds.
Thus, in line with what this coder found with R, the vectorized code ran more than twice as fast in Julia.
The Julia Optimization Mentality
This was a fun little exercise because I had no idea how it would turn out. Quite frankly, when I started I thought MATLAB would slightly edge out Julia when running such vectorized code. However, Julia continues to impress me. The only major problem that I had this time around was finding out to use the vec() function to deal with “1-dimensional matrices”, but once that was found I was able to get Julia to be faster than MATLAB, even though I know much more about MATLAB and this package itself is quite well optimized.
I think I should end on why I find the Julia philosophy compelling for scientific computing. The idea is not that “you have to devectorize to get the best code”, though there are situations where doing so can dramatically increase your speed. The idea is that you don’t have to contort yourself to vectorization to make everything work. In MATLAB, R, and Python, you have to vectorize in order to make your code to ever finish. That is not the case in Julia. Here, just write the code that seems natural and it will do really well. In this case, vectorized code was natural, and as you could see we got something that was even faster. To do better in MATLAB, we would at this stage have to start writing C/MEX code. In Julia, we could expand out the loops, play with adding SIMD calls, caching, etc. directly in the Julia language.
For scientific computing where we just want code that’s good enough to work, you can see it’s easier to get there with Julia. If you need to optimize it to be part of a library, you can optimize and devectorize it within Julia without having to go to C (many times by just adding macros throughout your code). Will it be as fast as C? No, but many tests show that you’ll at least get within a factor of two so, for almost every case, you might as well just code it in Julia and move on. Each blog post I do I am getting more and more converted!
The post Julia iFEM 2: Optimizing Stiffness Matrix Assembly appeared first on Stochastic Lifestyle.
