Re-posted from: http://www.stochasticlifestyle.com/multi-node-parallelism-in-julia-on-an-hpc/
Today I am going to show you how to parallelize your Julia code over some standard HPC interfaces. First I will go through the steps of parallelizing a simple code, and then running it with single-node parallelism and multi-node parallelism. The compute resources I will be using are the XSEDE (SDSC) Comet computer (using Slurm) and UC Irvine’s HPC (using SGE) to show how to run the code in two of the main job schedulers. You can follow along with the Comet portion by applying and getting a trial allocation.
First we need code
The code I am going to use to demonstrate this is a simple parallel for loop. The problem can be explained as follows: given a 2-dimensional polynomial  with coefficients
with coefficients  , find the area where
, find the area where 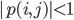 . The function for generating these coefficients in my actual code is quite wild, so for your purposes you can replace my coefficients by generating a random array of 36 numbers. Also it's a semi-sparse polynomial of at most degree 8 for each variable, so create arrays of powers powz and powk. We solve for the area by making a fine grid of
. The function for generating these coefficients in my actual code is quite wild, so for your purposes you can replace my coefficients by generating a random array of 36 numbers. Also it's a semi-sparse polynomial of at most degree 8 for each variable, so create arrays of powers powz and powk. We solve for the area by making a fine grid of  , evaluating the polynomial at each location, and summing up the places where its absolute value is less than 1.
, evaluating the polynomial at each location, and summing up the places where its absolute value is less than 1.
I developed this "simple" code for calculating this on my development computer:
julia -p 4
Opens Julia with 4 processes (or you can use addprocs(4) in your code), and then
dx = 1/400 imin = -8 imax = 1 jmin = -3 jmax = 3 coefs,powz,poww = getCoefficients(A0,A1,B0,B1,α,β1,β2,β3,β4) @time res = @sync @parallel (+) for i = imin:dx:imax tmp = 0 for j=jmin:dx:jmax ans = 0 @simd for k=1:36 @inbounds ans += coefs[k]*(i^(powz[k]))*(j^(poww[k])) end tmp += abs(ans)<1 end tmp end res = res*((imax-imin)*(jmax-jmin)/(length(imin:dx:imax)*length(jmin:dx:jmax))) println(res)
All that we did was loop over the grid $i$ and the grid of $j$, sum the polynomial, check if its absolute value is less than 1, check how many times it is less than 1, and scale by the area we integrated. Some things to note is that I first wrote the code out the "obvious way" and then added the macros to see if they would help. @inbounds turns off array bounds checking. @simd adds vectorization at the "processor" level (i.e. AVX2 to make multiple computations happen at once). @parallel runs the array in parallel and @sync makes the code wait for all processes to finish their part of the computation before moving on from the loop.
Note that this is not the most efficient code. The problem is that we re-use a lot of floating point operations in order to calculate the powers of  and
and  , so it actually works out much better to unravel the loop:
, so it actually works out much better to unravel the loop:
@time res = @sync @parallel (+) for i = imin:dx:imax tmp = 0 isq2 = i*i; isq3 = i*isq2; isq4 = isq2*isq2; isq5 = i*isq4 isq6 = isq4*isq2; isq7 = i*isq6; isq8 = isq4*isq4 @simd for j=jmin:dx:jmax jsq2 = j*j; jsq3= j*jsq2; jsq4 = jsq2*jsq2; jsq5 = j*jsq4; jsq6 = jsq2*jsq4; jsq7 = j*jsq6; jsq8 = jsq4*jsq4 @inbounds tmp += abs(coefs[1]*(jsq2) + coefs[2]*(jsq3) + coefs[3]*(jsq4) + coefs[4]*(jsq5) + coefs[5]*jsq6 + coefs[6]*jsq7 + coefs[7]*jsq8 + coefs[8]*(i) + coefs[9]*(i)*(jsq2) + coefs[10]*i*jsq3 + coefs[11]*(i)*(jsq4) + coefs[12]*i*jsq5 + coefs[13]*(i)*(jsq6) + coefs[14]*i*jsq7 + coefs[15]*(isq2) + coefs[16]*(isq2)*(jsq2) + coefs[17]*isq2*jsq3 + coefs[18]*(isq2)*(jsq4) + coefs[19]*isq2*jsq5 + coefs[20]*(isq2)*(jsq6) + coefs[21]*(isq3) + coefs[22]*(isq3)*(jsq2) + coefs[23]*isq3*jsq3 + coefs[24]*(isq3)*(jsq4) + coefs[25]*isq3*jsq5 + coefs[26]*(isq4) + coefs[27]*(isq4)*(jsq2) + coefs[28]*isq4*jsq3 + coefs[29]*(isq4)*(jsq4) + coefs[30]*(isq5) + coefs[31]*(isq5)*(jsq2) + coefs[32]*isq5*jsq3+ coefs[33]*(isq6) + coefs[34]*(isq6)*(jsq2) + coefs[35]*(isq7) + coefs[36]*(isq8))<1 end tmp end res = res*((imax-imin)*(jmax-jmin)/(length(imin:dx:imax)*length(jmin:dx:jmax))) println(res)
That's the fast version (for the powers I am using), and you can see how there simply are a lot less computations required by doing this. This gives almost a 10x speedup and is the fastest code I came up with. So now we're ready to put this on the HPC.
Setting up Comet
Log into Comet. I use the XSEDE single sign-on hub and gsissh into Comet from there. On Comet, you can download the generic 64-bit binary from here. You can also give compiling it a try yourself, it didn't work out to well for me and the generic binary worked fine. In order to do anything, you need to enter a compute node. To do this we open an interactive job with
srun -pty -p compute -t 01:00:00 -n24 /bin/bash -l
This gives you an interactive job with 24 cores (all on one node). Now we can actually compute things (if you tried before, you would have gotten an error). Now open up Julia by going to the appropriate directory and using
./julia -p 24
This will put you into an interactive session with 24 workers. Now install all your packages, etc., test your code, make sure everything is working.
Running Jobs
Now that Julia is all set up and you tested your code, you need to set up a job script. It's best explained via an example:
#!/bin/bash #SBATCH -A <account> #SBATCH --job-name="juliaTest" #SBATCH --output="juliaTest.%j.%N.out" #SBATCH --partition=compute #SBATCH --nodes=8 #SBATCH --export=ALL #SBATCH --ntasks-per-node=24 #SBATCH -t 01:00:00 export SLURM_NODEFILE=`generate_pbs_nodefile` ./julia --machinefile $SLURM_NODEFILE /home/crackauc/test.jl
In the first line you put the account name you were given when you signed up for Comet. This is the account whose time will be billed. Then you give your job a name and tell it where to save the output. Next is the partition that you wish to run on. Here I specify for it to be the compute node. Now I tell it the number of nodes. I wanted 8 nodes with 24 tasks per node. The time limit is 1 hour.
8 nodes? So we need to add some MPI code, right? NOPE! Julia does it for you! This is the amazing part. What we do is we export the Slurm node file and give it to Julia as the machinefile. This nodefile is simply a list of the compute nodes that are allocated to our job that is generated by the job manager. This will automatically open up one worker process for each thing in the node file (which will be 24 tasks per node, so there are 8*24= 192 lines in the node file and Julia will open up 192 processes) and run test.jl.
Did it work? A quick check is to have the following code in test.jl:
hosts = @parallel for i=1:192 println(run(`hostname`)) end
You should see it printout the names of 8 different hosts, each 24 times. This means our parallel loop automatically is on 192 cores!
Now add the code we made before to test.jl. When we run this in different settings, I get the following results: (SIMD is the first version, Full is the second "full unraveled" version)
8 Nodes:
SIMD - .74 seconds
Full - .324 seconds
4 Nodes:
SIMD - .77 seconds
Full - .21 seconds
2 Nodes:
SIMD - .81 seconds
Full - .21 seconds
1 Node
SIMD - .996 seconds
Full - .273 seconds
In this case we see that the optimal is to use 2 nodes. As you increase the domain you are integrating over / decrease  , you have to perform more computations which makes using more nodes more profitable. You can check yourself that if you use some extreme values like 1/1600 it may be better to use 4-8 nodes. But this ends our quick tutorial into multi-node parallelism on Comet. You're done. If you have ever programmed with MPI before, this is just beautiful.
, you have to perform more computations which makes using more nodes more profitable. You can check yourself that if you use some extreme values like 1/1600 it may be better to use 4-8 nodes. But this ends our quick tutorial into multi-node parallelism on Comet. You're done. If you have ever programmed with MPI before, this is just beautiful.
What about SGE?
Another popular job scheduler is SGE. They have this on my UC Irvine cluster. To use Julia with multi-nodes on this, you do pretty much the same thing. Here you have to tell it you want to do an MPI job. This will create the machine file and you stick that machine file into Julia. The job script is then as follows:
#!/bin/bash #$ -N jbtest #$ -q math #$ -pe mpich 128 #$ -cwd # run the job out of the current directory #$ -m beas #$ -ckpt blcr #$ -o output/ #$ -e output/ module load julia/0.4.3 julia --machinefile jbtest-pe_hostfile_mpich.$JOB_ID test.jl
That's it. SGE makes the machine file called jbtest-pe_hostfile_mpich.$JOB_ID which has the 128 processes to run (this is in the math queue, so for me it's split across 5 computers with the nodes repeated for the number of processes on that node), in your current directory, so I just load the Julia module and stick it into Julia as the machine file, test it out, and it prints out the name of compute nodes. On this computer I can even ssh into the nodes while a job is running to run htop. In htop I see that it uses as many cores on each computer that it says its using (sometimes a little bit more when it's using threading. You may need to set the number of BLAS threads to 0 if you are doing any linear algebra and don't want it to bleed). Success!
What about GPUs?
Using GPUs on this same problem is discussed in my next blog post!
The post Multi-node Parallelism in Julia on an HPC (XSEDE Comet) appeared first on Stochastic Lifestyle.
