By: Jan Vanhove
Re-posted from: https://janhove.github.io/posts/2023-03-07-julia-breakpoint-regression/index.html
In this fourth installment of Adjusting to Julia, I will at long last analyse some actual data. One of the first posts on this blog was Calibrating p-values in ‘flexible’ piecewise regression models. In that post, I fitted a piecewise regression to a dataset comprising the ages at which a number of language learners started learning a second language (age of acquisition, AOA) and their scores on a grammaticality judgement task (GJT) in that second language. A piecewise regression is a regression model in which the slope of the function relating the predictor (here: AOA) to the outcome (here: GJT) changes at some value of the predictor, the so-called breakpoint. The problem, however, was that I didn’t specify the breakpoint beforehand but pick the breakpoint that minimised the model’s deviance. This increased the probability that I would find that the slope before and after the breakpoint differed, even if they in fact were the same. In the blog post I wrote almost nine years ago, I sought to recalibrate the p-value for the change in slope by running a bunch of simulations in R. In this blog post, I’ll do the same, but in Julia.
The data set
We’ll work with the data from the North America study conducted by DeKeyser et al. (2010). If you want to follow along, you can download this dataset here and save it to a subdirectory called data in your working directory.
We need the DataFrames, CSV and StatsPlots packages in order to read in the CSV with the dataset as a data frame and draw some basic graphs.
using DataFrames, CSV, StatsPlots
d = CSV.read("data/dekeyser2010.csv", DataFrame);
@df d plot(:AOA, :GJT
, seriestype = :scatter
, legend = :none
, xlabel = "AOA"
, ylabel = "GJT")
The StatsPlots package uses the @df macro to specify that the variables in the plot() function can be found in the data frame provided just after it (i.e., d).
Two regression models
Let’s fit two regression models to this data set using the GLM package. The first model, lm1, is a simple regression model with AOA as the predictor and GJT as the outcome. The syntax should be self-explanatory:
using GLM
lm1 = lm(@formula(GJT ~ AOA), d);
coeftable(lm1)
| (Intercept) |
190.409 |
3.90403 |
48.77 |
<1e-57 |
182.63 |
198.188 |
| AOA |
-1.21798 |
0.105139 |
-11.58 |
<1e-17 |
-1.42747 |
-1.00848 |
We can visualise this model by plotting the data in a scatterplot and adding the model predictions to it like so. I use begin and end to force Julia to only produce a single plot.
d[!, "prediction"] = predict(lm1);
begin
@df d plot(:AOA, :GJT
, seriestype = :scatter
, legend = :none
, xlabel = "AOA"
, ylabel = "GJT");
@df d plot!(:AOA, :prediction
, seriestype = :line)
end
Our second model will incorporate an ‘elbow’ in the regression line at a given breakpoint – a piecewise regression model. For a breakpoint bp, we need to create a variable since_bp that encodes how many years beyond this breakpoint the participants’ AOA values are. If an AOA value is lower than the breakpoint, the corresponding since_bp value is just 0. The add_breakpoint() value takes a dataset containing an AOA variable and adds a variable called since_bp to it.
function add_breakpoint(data, bp)
data[!, "since_bp"] = max.(0, data[!, "AOA"] .- bp);
end;
To add the since_bp variable for a breakpoint at age 12 to our dataset d, we just run this function. Note that in Julia, arguments are not copied when they are passed to a function. That is, the add_breakpoint() function changes the dataset; it does not create a changed copy of the dataset like R would:
# changes d!
add_breakpoint(d, 12);
print(d);
76×4 DataFrame
Row │ AOA GJT prediction since_bp
│ Int64 Int64 Float64 Int64
─────┼────────────────────────────────────
1 │ 59 151 118.548 47
2 │ 9 182 179.447 0
3 │ 51 127 128.292 39
4 │ 58 113 119.766 46
5 │ 27 157 157.523 15
6 │ 11 188 177.011 0
7 │ 17 125 169.703 5
8 │ 57 138 120.984 45
9 │ 10 171 178.229 0
10 │ 14 168 173.357 2
11 │ 20 174 166.049 8
12 │ 34 149 148.997 22
13 │ 19 155 167.267 7
14 │ 54 149 124.638 42
15 │ 63 107 113.676 51
16 │ 71 104 103.932 59
17 │ 24 176 161.177 12
18 │ 16 143 170.921 4
19 │ 22 133 163.613 10
20 │ 48 113 131.946 36
21 │ 17 171 169.703 5
22 │ 20 144 166.049 8
23 │ 44 151 136.818 32
24 │ 24 182 161.177 12
25 │ 56 113 122.202 44
26 │ 5 197 184.319 0
27 │ 71 114 103.932 59
28 │ 36 170 146.561 24
29 │ 57 115 120.984 45
30 │ 45 115 135.6 33
31 │ 56 118 122.202 44
32 │ 44 118 136.818 32
33 │ 23 155 162.395 11
34 │ 18 186 168.485 6
35 │ 42 132 139.254 30
36 │ 54 116 124.638 42
37 │ 14 169 173.357 2
38 │ 47 131 133.164 35
39 │ 8 196 180.665 0
40 │ 24 122 161.177 12
41 │ 52 148 127.074 40
42 │ 27 188 157.523 15
43 │ 11 198 177.011 0
44 │ 18 174 168.485 6
45 │ 48 150 131.946 36
46 │ 31 158 152.651 19
47 │ 49 131 130.728 37
48 │ 48 131 131.946 36
49 │ 15 180 172.139 3
50 │ 49 113 130.728 37
51 │ 23 167 162.395 11
52 │ 10 193 178.229 0
53 │ 20 164 166.049 8
54 │ 24 183 161.177 12
55 │ 35 118 147.779 23
56 │ 36 136 146.561 24
57 │ 44 115 136.818 32
58 │ 49 141 130.728 37
59 │ 15 181 172.139 3
60 │ 12 193 175.793 0
61 │ 53 140 125.856 41
62 │ 16 153 170.921 4
63 │ 54 110 124.638 42
64 │ 9 163 179.447 0
65 │ 25 174 159.959 13
66 │ 27 169 157.523 15
67 │ 18 179 168.485 6
68 │ 26 143 158.741 14
69 │ 22 162 163.613 10
70 │ 50 128 129.51 38
71 │ 42 119 139.254 30
72 │ 5 197 184.319 0
73 │ 14 168 173.357 2
74 │ 39 132 142.908 27
75 │ 56 140 122.202 44
76 │ 12 182 175.793 0
Since we don’t know what the best breakpoint is, we’re going to estimate it from the data. For each integer in a given range (minbp through maxbp), we’re going to fit a piecewise regression model with that integer as the breakpoint. We’ll then pick the breakpoint that minimises the deviance of the fit (i.e., the sum of squared differences between the model fit and the actual outcome). The fit_piecewise() function takes care of this. It outputs both the best fitting piecewise regression model and the breakpoint used for this model.
function fit_piecewise(data, minbp, maxbp)
min_deviance = Inf
best_model = nothing
best_bp = 0
current_model = nothing
for bp in minbp:maxbp
add_breakpoint(data, bp)
current_model = lm(@formula(GJT ~ AOA + since_bp), data)
if deviance(current_model) < min_deviance
min_deviance = deviance(current_model)
best_model = current_model
best_bp = bp
end
end
return best_model, best_bp
end;
Let’s now apply this function to our dataset. The estimated breakpoint is at age 16, and the model coefficients are shown below:
lm2 = fit_piecewise(d, 6, 20);
# the first output is the model itself, the second the breakpoint used
coeftable(lm2[1])
lm2[2]
Let’s visualise this model by drawing a scatterplot and adding the regression fit to it. While we’re at it, we might as well add a 95% confidence band around the regression fit.
add_breakpoint(d, 16);
predictions = predict(lm2[1], d;
interval = :confidence,
level = 0.95);
d[!, "prediction"] = predictions[!, "prediction"];
d[!, "lower"] = predictions[!, "lower"];
d[!, "upper"] = predictions[!, "upper"];
begin
@df d plot(:AOA, :GJT
, seriestype = :scatter
, legend = :none
, xlabel = "AOA"
, ylabel = "GJT"
);
@df d plot!(:AOA, :prediction
, seriestype = :line
, ribbon = (:prediction .- :lower,
:upper .- :prediction)
)
end
We could run an 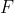 -test for the model comparison like below, but the
-test for the model comparison like below, but the 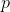 -value corresponds to the
-value corresponds to the 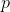 -value for the
-value for the since_bp value, anyway:
ftest(lm1.model, lm2[1].model);
But there’s a problem: This 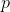 -value can’t be taken at face value. By looping through different possible breakpoint and then picking the one that worked best for our dataset, we’ve increased our chances of finding some pattern in the data even if nothing is going on. So we need to recalibrate the
-value can’t be taken at face value. By looping through different possible breakpoint and then picking the one that worked best for our dataset, we’ve increased our chances of finding some pattern in the data even if nothing is going on. So we need to recalibrate the 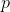 -value we’ve obtained.
-value we’ve obtained.
Recalibrating the p-value
Our strategy is as follows. We will generate a fairly large number of datasets similar to d but of which we know that there isn’t any breakpoint in the GJT/AOA relationship. We will do this by simulating new GJT values from the simple regression model fitted above (lm1). We will then apply the fit_piecewise() function to each of these datasets, using the same minbp and maxbp values as before and obtain the 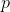 -value associated with each model. We will then compute the proportion of the
-value associated with each model. We will then compute the proportion of the 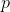 -value so obtained that is lower than the
-value so obtained that is lower than the 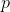 -value from our original model, i.e., 0.0472.
-value from our original model, i.e., 0.0472.
I wasn’t able to find a Julia function similar to R’s simulate() that simulates a new outcome variable based on a linear regression model. But such a function is easy enough to put together:
using Distributions
function simulate_outcome(null_model)
resid_distr = Normal(0, dispersion(null_model.model))
prediction = fitted(null_model)
new_outcome = prediction + rand(resid_distr, length(prediction))
return new_outcome
end;
The one_run() function generates a single new outcome vector, overwrites the GJT variable in our dataset with it, and then applies the fit_piecewise() function to the dataset, returning the 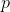 -value of the best-fitting piecewise regression model.
-value of the best-fitting piecewise regression model.
function one_run(data, null_model, min_bp, max_bp)
new_outcome = simulate_outcome(null_model)
data[!, "GJT"] = new_outcome
best_model = fit_piecewise(data, min_bp, max_bp)
pval = coeftable(best_model[1]).cols[4][3]
return pval
end;
Finally, the generate_p_distr() function runs the one_run() function a large number of times and output the 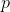 -values generated.
-values generated.
function generate_p_distr(data, null_model, min_bp, max_bp, n_runs)
pvals = [one_run(data, null_model, min_bp, max_bp) for _ in 1:n_runs]
return pvals
end;
Our simulation will consist of 25,000 runs, and in each run, 16 regression models will be fitted, for a total of 400,000 models. On my machine, this takes less than 20 seconds (i.e., less than 50 microseconds per model).
n_runs = 25_000;
pvals = generate_p_distr(d, lm1, 6, 20, n_runs);
For about 11–12% of the datasets in which no breakpoint governed the data, the fit_piecewise() procedure returned a 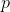 -value of 0.0472 or lower. So our original
-value of 0.0472 or lower. So our original 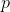 -value of 0.0472 ought to be recalibrated to about 0.12.
-value of 0.0472 ought to be recalibrated to about 0.12.
sum(pvals .<= 0.0472) / n_runs