Tag Archives: General

Data Wrangling in Julia based on dplyr Flights Tutorials

Re-posted from: https://cbrownley.wordpress.com/2017/11/29/data-wrangling-in-julia-based-on-dplyr-flights-tutorials/

A couple of my favorite tutorials for wrangling data in R with dplyr are Hadley Wickham’s dplyr package vignette and Kevin Markham’s dplyr tutorial. I enjoy the tutorials because they concisely illustrate how to use a small set of verb-based functions to carry out common data wrangling tasks.

I tend to use Python to wrangle data, but I’m exploring the Julia programming language so I thought creating a similar dplyr-based tutorial in Julia would be a fun way to examine Julia’s capabilities and syntax. Julia has several packages that make it easier to deal with tabular data, including DataFrames and DataFramesMeta.

The DataFrames package provides functions for reading and writing, split-apply-combining, reshaping, joining, sorting, querying, and grouping tabular data. The DataFramesMeta package provides a set of macros that are similar to dplyr’s verb-based functions in that they offer a more convenient, readable syntax for munging data and chaining together multiple operations.

Data

For this tutorial, let’s following along with Kevin’s tutorial and use the hflights dataset. You can obtain the dataset from R with the following commands or simply download it here: hflights.csv

install.packages("hflights") library(hflights) write.csv(hflights, "hflights.csv")

Load packages and example dataset

To begin, let’s start the Julia REPL, load the DataFrames and DataFramesMeta packages, and load and inspect the hflights dataset:

using DataFrames using DataFramesMeta

hflights = readtable("/Users/clinton/Documents/Julia/hflights.csv"); size(hflights) names(hflights) head(hflights) describe(hflights)

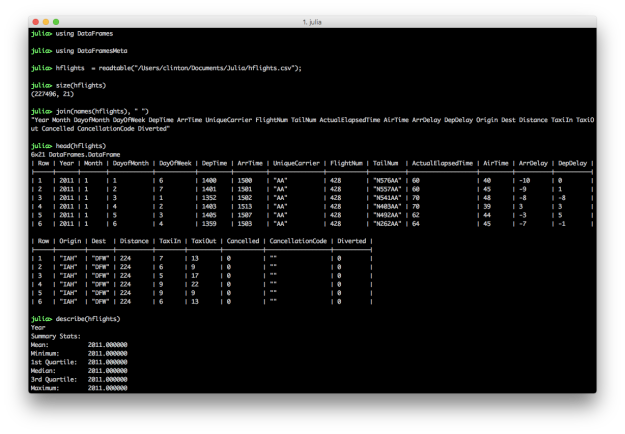
hflights1b

The semicolon on the end of the readtable command prevents it from printing the dataset to the screen. The size command returns the number of rows and columns in the dataset. You can specify you only want the number of rows with size(hflights, 1) or columns with size(hflights, 2). This dataset contains 227,496 rows and 21 columns. The names command lists the column headings. By default, the head command prints the header row and six data rows. You can specify the number of data rows to display by adding a second argument, e.g. head(hflights, 10). The describe command prints summary statistics for each column.

@where: Keep rows matching criteria

AND: All of the conditions must be true for the returned rows

# Julia DataFrames approach to view all flights on January 1 hflights[.&(hflights[:Month] .== 1, hflights[:DayofMonth] .== 1), :]

# DataFramesMeta approach @where(hflights, :Month .== 1, :DayofMonth .== 1)

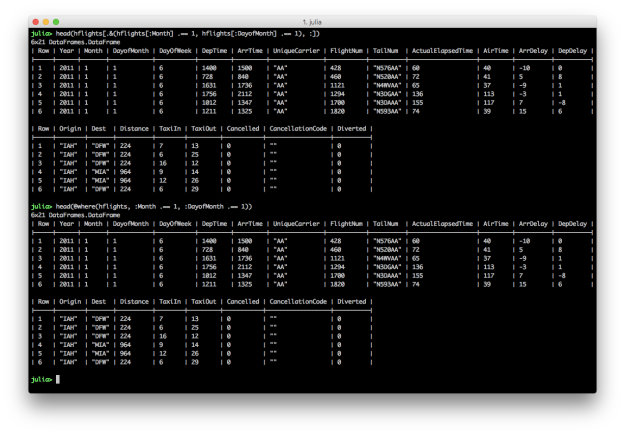
hflights2

Julia’s DataFrames’ row filtering syntax is similar to R’s syntax. To specify multiple AND conditions, use “.&()” and place the filtering conditions, separated by commas, between the parentheses. Like dplyr’s filter function, DataFramesMeta’s @where macro simplifies the syntax and makes the command easier to read.

OR: One of the conditions must be true for the returned rows

# Julia DataFrames approach to view all flights where either AA or UA is the carrier hflights[.|(hflights[:UniqueCarrier] .== "AA", hflights[:UniqueCarrier] .== "UA"), :]

# DataFramesMeta approach @where(hflights, .|(:UniqueCarrier .== "AA", :UniqueCarrier .== "UA"))

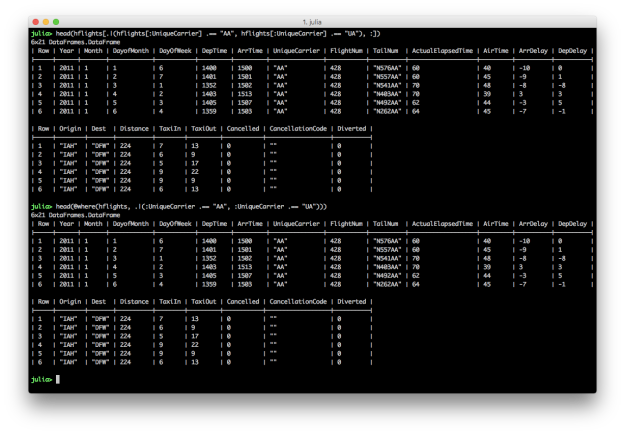
hflights3

To specify multiple OR conditions, use “.|()” and place the filtering conditions between the parentheses. Again, the DataFramesMeta approach is more concise.

SET: The values in a column are in a set of interest

# Julia DataFrames approach to view all flights where the carrier is in Set(["AA", "UA"]) carriers_set = Set(["AA", "UA"]) hflights[findin(hflights[:UniqueCarrier], carriers_set), :]

# DataFramesMeta approach @where(hflights, findin(:UniqueCarrier, carriers_set))

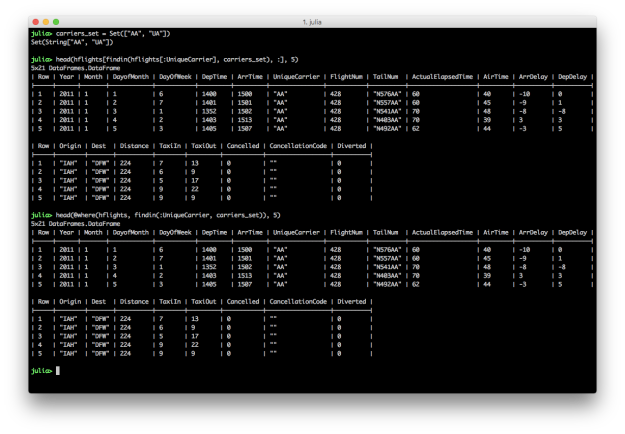
hflights4

To filter for rows where the values in a particular column are in a specific set of interest, create a Set with the values you’re interested in and then specify the column and your set of interest in the findin function.

PATTERN / REGULAR EXPRESSION: The values in a column match a pattern

# Julia DataFrames approach to view all flights where the carrier matches the regular expression r"AA|UA" carriers_pattern = r"AA|UA" hflights[[ismatch(carriers_pattern, String(carrier)) for carrier in hflights[:UniqueCarrier]], :]

# DataFramesMeta approach @where(hflights, [ismatch(carriers_pattern, String(carrier)) for carrier in :UniqueCarrier])

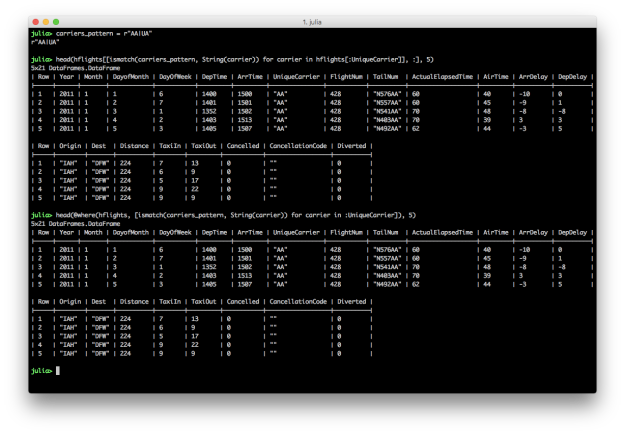
hflights5

To filter for rows where the values in a particular column match a pattern, create a regular expression and then use it in the ismatch function in an array comprehension.

@select: Pick columns by name

# Julia DataFrames approach to selecting columns hflights[:, [:DepTime, :ArrTime, :FlightNum]]

# DataFramesMeta approach @select(hflights, :DepTime, :ArrTime, :FlightNum)

Julia’s DataFrames’ syntax for selecting columns is similar to R’s syntax. Like dplyr’s select function, DataFramesMeta’s @select macro simplifies the syntax and makes the command easier to read.

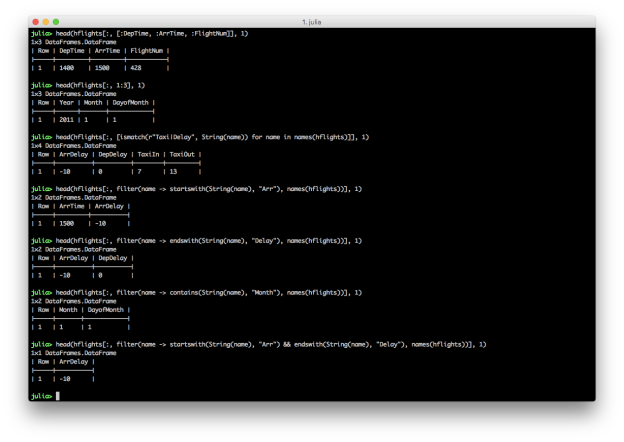
# Julia DataFrames approach to selecting columns # first three columns hflights[:, 1:3] # pattern / regular expression heading_pattern = r"Taxi|Delay" hflights[:, [ismatch(heading_pattern, String(name)) for name in names(hflights)]] # startswith hflights[:, filter(name -> startswith(String(name), "Arr"), names(hflights))] # endswith hflights[:, filter(name -> endswith(String(name), "Delay"), names(hflights))] # contains hflights[:, filter(name -> contains(String(name), "Month"), names(hflights))]

# AND conditions hflights[:, filter(name -> startswith(String(name), "Arr") && endswith(String(name), "Delay"), names(hflights))] # OR conditions hflights[:, filter(name -> startswith(String(name), "Arr") || contains(String(name), "Cancel"), names(hflights))]

hflights6

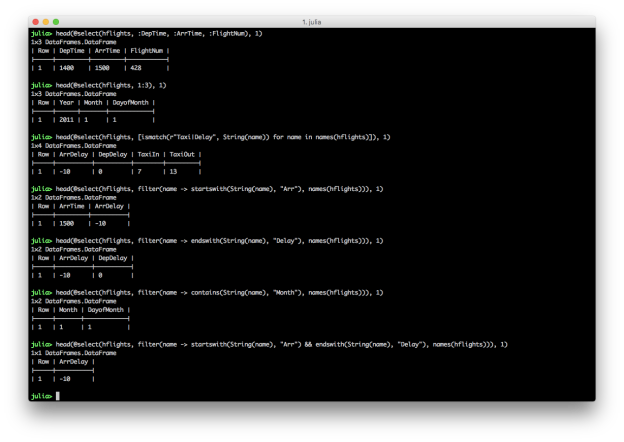
# DataFramesMeta approach # first three columns @select(hflights, 1:3) # pattern / regular expression heading_pattern = r"Taxi|Delay" @select(hflights, [ismatch(heading_pattern, String(name)) for name in names(hflights)]) # startswith @select(hflights, filter(name -> startswith(String(name), "Arr"), names(hflights))) # endswith @select(hflights, filter(name -> endswith(String(name), "Delay"), names(hflights))) # contains @select(hflights, filter(name -> contains(String(name), "Month"), names(hflights)))

# AND conditions @select(hflights, filter(name -> startswith(String(name), "Arr") && endswith(String(name), "Delay"), names(hflights))) # OR conditions @select(hflights, filter(name -> startswith(String(name), "Arr") || contains(String(name), "Cancel"), names(hflights)))

hflights7

# Kevin Markham's multiple select conditions example # select(flights, Year:DayofMonth, contains("Taxi"), contains("Delay")) # Julia Version of Kevin's Example # Taxi or Delay in column heading mask = [ismatch(r"Taxi|Delay", String(name)) for name in names(hflights)] # Also include first three columns, i.e. Year, Month, DayofMonth mask[1:3] = true @select(hflights, mask)

These examples show you can select columns by position and name, and you can combine multiple conditions with AND, “&&”, or OR, “||”. Similar to filtering rows, you can select specific columns based on a pattern by using the ismatch function in an array comprehension. You can also use contains, startswith, and endswith in the filter function to select columns that contain, start with, or end with a specific text pattern.

“Chaining” or “Pipelining”

In R, dplyr provides, via the magrittr package, the %>% operator, which enables you to chain together multiple commands into a single data transformation pipeline in a very readable fashion. In Julia, the DataFramesMeta package provides the @linq macro and |> symbol to enable similar functionality. Alternatively, you can load the Lazy package and use an @> begin end block to chain together multiple commands.

# Chaining commands with DataFrameMeta’s @linq macro @linq hflights[find(.!isna.(hflights[:,:DepDelay])), :] |> @where(:DepDelay .> 60) |> @select(:UniqueCarrier, :DepDelay)

# Chaining commands with Lazy’s @> begin end block using Lazy @> begin hflights[find(.!isna.(hflights[:,:DepDelay])), :] @where(:DepDelay .> 60) @select(:UniqueCarrier, :DepDelay) end

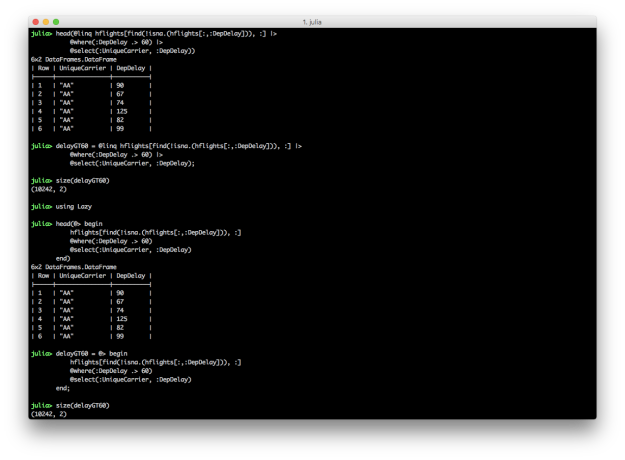
hflights8

These two blocks of code produce the same result, a DataFrame containing carrier names and departure delays for which the departure delay is greater than 60. In each chain, the first expression is the input DataFrame, e.g. hflights. In these examples, I use the find and !isna. functions to start with a DataFrame that doesn’t contain NA values in the DepDelay column because the commands fail when NAs are present. I prefer the @linq macro version over the @> begin end version because it’s so similar to the dplyr-magrittr syntax, but both versions are more succinct and readable than their non-chained versions. The screen shot shows how to assign the pipeline results to variables.

@orderby: Reorder rows

Both DataFrames and DataFramesMeta provide functions for sorting rows in a DataFrame by values in one or more columns. In the first pair of examples, we want to select the UniqueCarrier and DepDelay columns and then sort the results by the values in the DepDelay column in descending order. The last example shows how to sort by multiple columns with the @orderby macro.

# Julia DataFrames approach to sorting sort(hflights[find(.!isna.(hflights[:,:DepDelay])), [:UniqueCarrier, :DepDelay]], cols=[order(:DepDelay, rev=true)])

# DataFramesMeta approach (add a minus sign before the column symbol for descending) @linq hflights[find(.!isna.(hflights[:,:DepDelay])), :] |> @select(:UniqueCarrier, :DepDelay) |> @orderby(-:DepDelay)

# Sort hflights dataset by Month, descending, and then by DepDelay, ascending @linq hflights |> @orderby(-:Month, :DepDelay)

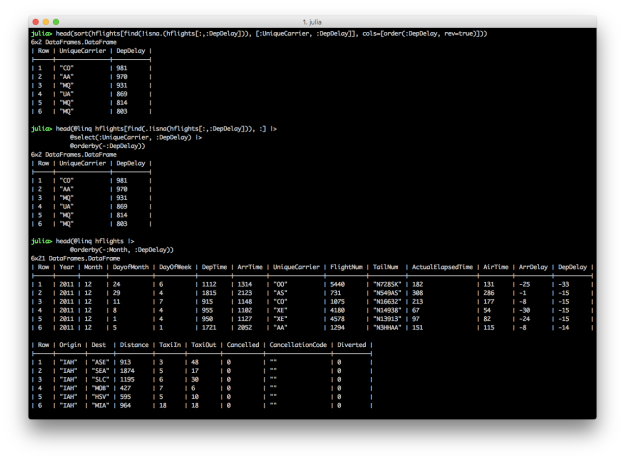
hflights9

DataFrames provides the sort and sort! functions for ordering rows in a DataFrame. sort! orders the rows, inplace. The DataFrames user guide provides additional examples of ordering rows, in ascending and descending order, based on multiple columns, as well as applying functions to columns, e.g. uppercase, before using the column for sorting.

DataFramesMeta provides the @orderby macro for ordering rows in a DataFrame. Specify multiple column names in the @orderby macro to sort the rows by multiple columns. Use a minus sign before a column name to sort in descending order.

@transform: Add new variables

Creating new variables in Julia DataFrames is similar to creating new variables in Python and R. You specify a new column name in square brackets after the name of the DataFrame and assign it a collection of values, sometimes based on values in other columns. DataFramesMeta’s @transform macro simplifies the syntax and makes the transformation more readable.

# Julia DataFrames approach to creating new variable hflights[:Speed] = hflights[:Distance] ./ hflights[:AirTime] .* 60 hflights[:, [:Distance, :AirTime, :Speed]]

# Delete the variable so we can recreate it with DataFramesMeta approach delete!(hflights, :Speed)

# DataFramesMeta approach @linq hflights |> @select(:Distance, :AirTime) |> @transform(Speed = :Distance ./ :AirTime .* 60) |> @select(:Distance, :AirTime, :Speed)

# Save the new column in the original DataFrame hflights = @linq hflights |> @transform(Speed = :Distance ./ :AirTime .* 60)

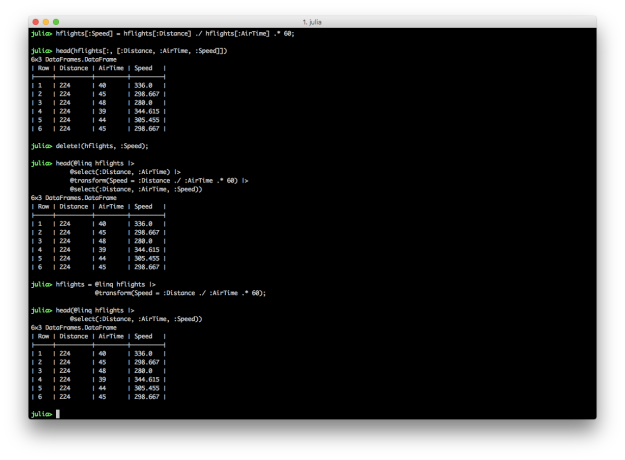
hflights10

The first code block illustrates how to create a new column in a DataFrame and assign it values based on values in other columns. The second code block shows you can use delete! to delete a column. The third example demonstrates the DataFramesMeta approach to creating a new column using the @transform macro. The last example shows how to save a new column in an existing DataFrame using the @transform macro by assigning the result of the transformation to the existing DataFrame.

@by: Reduce variables to values (Grouping and Summarizing)

dplyr provides group_by and summarise functions for grouping and summarising data. DataFrames and DataFramesMeta also support the split-apply-combine strategy with the by function and the @by macro, respectively. Here Julia versions of Kevin’s summarise examples.

# Julia DataFrames approach to grouping and summarizing by(hflights[complete_cases(hflights[[Symbol(name) for name in names(hflights)]]), :], :Dest, df -> DataFrame(meanArrDelay = mean(df[:ArrDelay])))

# DataFramesMeta approach @linq hflights[complete_cases(hflights[[Symbol(name) for name in names(hflights)]]), :] |> @by(:Dest, meanArrDelay = mean(:ArrDelay))

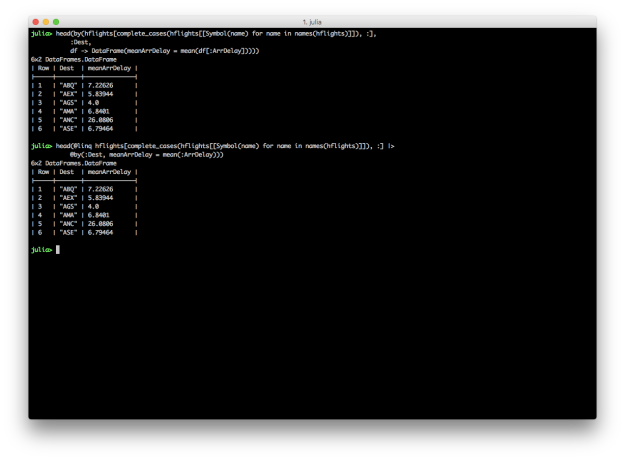
hflights11

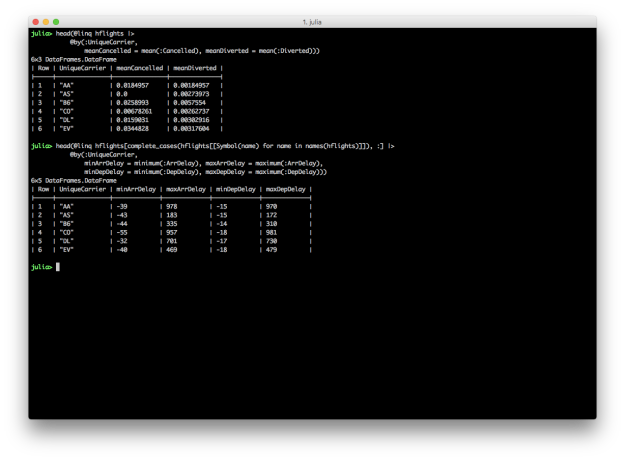
DataFrames and DataFramesMeta don’t have dplyr’s summarise_each function, but it’s easy to apply different functions to multiple columns inside the @by macro.

@linq hflights |> @by(:UniqueCarrier, meanCancelled = mean(:Cancelled), meanDiverted = mean(:Diverted))

@linq hflights[complete_cases(hflights[[Symbol(name) for name in names(hflights)]]), :] |> @by(:UniqueCarrier, minArrDelay = minimum(:ArrDelay), maxArrDelay = maximum(:ArrDelay), minDepDelay = minimum(:DepDelay), maxDepDelay = maximum(:DepDelay))

hflights12

DataFrames and DataFramesMeta also don’t have dplyr’s n and n_distinct functions, but you can count the number of rows in a group with size(df, 1) or nrow(df), and you can count the number of distinct values in a group with countmap.

# Group by Month and DayofMonth, count the number of flights, and sort descending # Count the number of rows with size(df, 1) sort(by(hflights, [:Month,:DayofMonth], df -> DataFrame(flight_count = size(df, 1))), cols=[order(:flight_count, rev=true)])

# Group by Month and DayofMonth, count the number of flights, and sort descending # Count the number of rows with nrow(df) sort(by(hflights, [:Month,:DayofMonth], df -> DataFrame(flight_count = nrow(df))), cols=[order(:flight_count, rev=true)])

# Split grouping and sorting into two separate operations g = by(hflights, [:Month,:DayofMonth], df -> DataFrame(flight_count = nrow(df))) sort(g, cols=[order(:flight_count, rev=true)])

# For each destination, count the total number of flights and the number of distinct planes by(hflights[find(.!isna.(hflights[:,:TailNum])),:], :Dest) do df DataFrame(flight_count = size(df,1), plane_count = length(keys(countmap(df[:,:TailNum])))) end

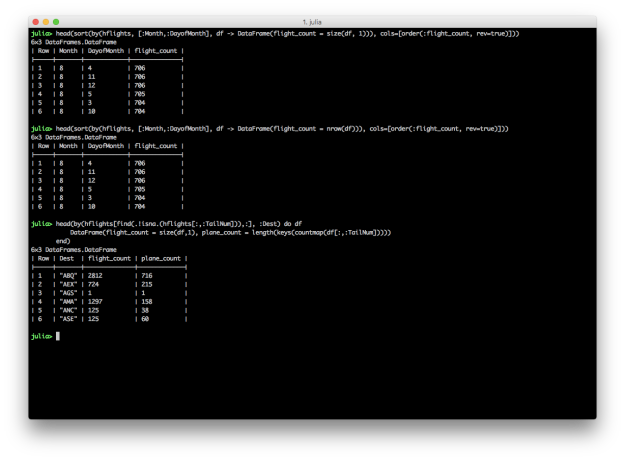
hflights13

While these examples reproduce the results in Kevin’s dplyr tutorial, they’re definitely not as succinct and readable as the dplyr versions. Grouping by multiple columns, summarizing with counts and distinct counts, and gracefully chaining these operations are areas where DataFrames and DataFramesMeta can improve.

Other useful convenience functions

Randomly sampling a fixed number or fraction of rows from a DataFrame can be a helpful operation. dplyr offers the sample_n and sample_frac functions to perform these operations. In Julia, StatsBase provides the sample function, which you can repurpose to achieve similar results.

using StatsBase # randomly sample a fixed number of rows hflights[sample(1:nrow(hflights), 5), :] hflights[sample(1:size(hflights,1), 5), :]

# randomly sample a fraction of rows hflights[sample(1:nrow(hflights), ceil(Int,0.0001*nrow(hflights))), :] hflights[sample(1:size(hflights,1), ceil(Int,0.0001*size(hflights,1))), :]

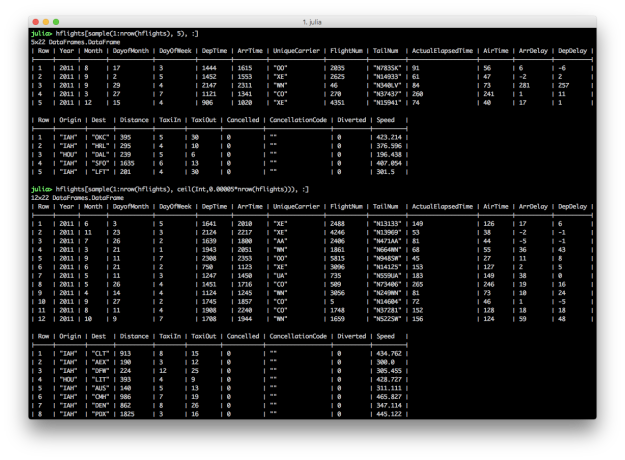
hflights14

Randomly sampling a fixed number of rows is fairly straightforward. You use the sample function to randomly select a fixed number of rows, in this case five, from the DataFrame. Randomly sampling a fraction of rows is slightly more complicated because, since the sample function takes an integer for the number of rows to return, you need to use the ceil function to convert the fraction of rows, in this case 0.0001*nrow(hflights), into an integer.

Conclusion

In R, dplyr sets a high bar for wrangling data well with succinct, readable code. In Julia, DataFrames and DataFramesMeta provide many useful functions and macros that produce similar results; however, some of the syntax isn’t as concise and clear as it is with dplyr, e.g. selecting columns in different ways and chaining together grouping and summarizing operations. These are areas where Julia’s packages can improve.

I enjoyed becoming more familiar with Julia by reproducing much of Kevin’s dplyr tutorial. It was also informative to see differences in functionality and readability between dplyr and Julia’s packages. I hope you enjoyed this tutorial and find it to be a useful reference for wrangling data in Julia.

Filed under: Analytics, General, Julia, Python, R, Statistics Tagged: DataFrames, DataFramesMeta, dplyr, Julia, Python, R

Computationally Visualizing Crystals

Christina C. Lee, github: albi3ro

Prerequisites: none

In condensed matter, we find ourselves in the interesting middle ground of dealing with large numbers, e.g. $10^{23}$ , of extremely small particles such as atoms, or electrons.

Luckily, the particles don’t each do their own thing, but often come in nice, structured, repeated units. Lattices. As our first step into the field, we will look at the most basic type, a Bravais lattice.

In a Bravais lattice, every site looks like every other site. Mathematically, we use three vectors, $vec{a},vec{b},vec{c}$ to express how we move from one site to a neighbor.

begin{equation}
mathbf{R}_{lmn}=l vec{a} + m vec{b} + n vec{c} ;;;; text{for } l,m,n in mathbb{N}
end{equation}

For consistency, we have to put a constraint on these vectors; we cannot combine two of the vectors and obtain the third. If we could, then we couldn’t have sites in an entire three dimensional space.

Stay tuned for a later post where we explore more elaborate lattices.

# importing our packages
Pkg.add("PyPlot");
Pkg.update();
using PyPlot;

Define The Relevant Variables

Choose the lattice you want to look at, and use that string for the lattice variable.
Current options:

Simple Cubic = “sc”
Plane triangular lattice = “pt”
Body-Centered Cubic = “bcc”
Face-Centered Cubic = “fcc”

Note: Square is Simple Cubic for Nz=1

14 distinct lattice types are possible, but these common four give the important ideas.

Also, input the size of lattice you want to look at.

lattice="sc";

Nx=3;
Ny=3;
Nz=3;

# A cell to just evaluate
# This one sets the unit vectors (a,b,c) for the different unit cells
# Can you guess what a lattice will look like by looking at the vectors?
if(lattice=="sc")
    d=3;
    a=[1,0,0];
    b=[0,1,0];
    c=[0,0,1];
elseif(lattice=="pt")
    d=2;
    a=[1,0,0];
    b=[.5,sqrt(3)/2,0];
    c=[0,0,1];
elseif(lattice=="bcc")
    d=3;
    a=[.5,.5,.5];
    b=[.5,.5,-.5];
    c=[.5,-.5,.5];
elseif(lattice=="fcc")
    d=3;
    a=[.5,.5,0];
    b=[.5,0,.5];
    c=[0,.5,.5];
else
    println("Please have a correct lattice")
end

# Another cell to just evaluate
# Here we set up some numbers and matrices for our computation
N=Nx*Ny*Nz;    #The total number of sites
aM=transpose(a);
bM=transpose(repeat(b,outer=[1,Nx])); #these allow us to copy an entire row or layer at once
cM=transpose(repeat(c,outer=[1,Nx*Ny]));

X=Array{Float64}(N,3);  #where we store the positions

# Another cell to just evaluate
# Here we are actually calculating the positions for every site
for i in 1:Nx    #for the first row
    X[i,:]=(i-1)*a;
end

for j in 2:Ny    #copying the first row into the first layer
    X[Nx*(j-1)+(1:Nx),:]=X[1:Nx,:]+(j-1)*bM;
end

for j in 2:Nz    #copying the first layer into the entire cube
    X[Ny*Nx*(j-1)+(1:Nx*Ny),:]=X[1:Nx*Ny,:]+(j-1)*cM;
end

Programming Tip:

In Julia, ranges, like 1:Nx, are a special variable type that can be manipulated. We can add numbers to them:
3+(1:3)=4:6,
or add a minus sign to force it to iterate in the opposite direction, though with different start/stop:
-(1:3)=-1:-1:-3

Danger! Make sure to use the parentheses around the range if you are performing these operations.

pygui(false);  #if true, launches new window with interactive capabilities

drawcube=true;  #gives lines for a cube, helps interpret the dots
ls=2;  # how many cubes to draw
if(drawcube==true)
    v=collect(0:ls);
    zed=zeros(v);
    for i in 0:ls
        for j in 0:ls
            plot3D(zed+i,v,zed+j)
            plot3D(zed+i,zed+j,v)

            plot3D(v,zed+i,zed+j)
            plot3D(zed+j,zed+i,v)

            plot3D(v,zed+j,zed+i)
            plot3D(zed+j,v,zed+i)
        end
    end
end

scatter3D(X[:,1],X[:,2],X[:,3],s=200*ones(X[:,1]),alpha=1)

Simple Cubic: The easiest lattice out there short of the 1D chain.

Point Triangular: A 2D lattice. Plotted using scatter instead of scatter3D.

bcc

Body Centered Cubic: Notice how some sites fall on the cubic lattice, but others fall in between. Generated with pygui(true) and then manipulating in 3D.

fcc

Face Centered Cubic: Here the sites either fall on the the cubic corners of in the center of the sides. Generated with pygui(true), ls=1, and then manipulating in 3D.

Go Back and Fiddle!

As you might have noticed, this isn’t just a blog where you read through the posts. Interact with it. Change some lines, and see what happens. I choose body centered cubic to display first, but what do the other lattices look like?

Chose pygui(true) to pop open a window and manipulate the plot in 3D.

Look at different lattice sizes.

Can you hand draw them on paper?

handdrawn fcc

A face centered cubic I decided to draw myself.

Let me know what you think, and enjoy the sequel as well!

Multi-site unit cells

Computationally Visualizing Crystals Pt. 2

Christina C. Lee, github: albi3ro

Prerequisites: Computationally Visualizing Crystals Pt. 1

Time to one-up the Bravais lattice from Part 1. Many beautiful lattices don’t adhere to the “every site the same” policy. They still repeat, but just take a little bit longer to get around to doing so.

Take the Kagome Lattice below,

kagome

A Kagome Lattice.

basket

A basket woven in the Japanese kagome style. _{Wikimedia commons}

If we look at the stars at the center of triangles, we can recognize a point triangular Bravais lattice. Now each of those stars stands for a grouping of three sites in a unit cell. According to Chem Wiki, a unit cell is:

A unit cell is the most basic and least volume consuming repeating structure of any solid. It is used to visually simplify the crystalline patterns solids arrange themselves in.

I chose these triangles to be be the unit cells above and in my computational representation below, but can you think of any other ways to represent the unit cell?

Turns out, there isn’t a unique way. We can go further and define the Wigner-Seitz unit cell, which uses the Bravais translations to pick out just ONE of the various possible definitions.

In my line of work though, we often use either the easiest to write down, or the one that has the symmetries we want.

Introducing Some Lattice Options

You saw Kagome above.

The options I’ve put in now are:

honeycomb
kagome
shuriken (a.k.a. square-Kagome)
diamond
pyrochlore

The ones implemented here, except for diamond, are frustrated lattices that I work with in my research. Honeycomb is well known in condensed matter physics for being the structure of graphene. This is an extremely important material right now, though I work with it in terms of the Kitaev spin model (to be discussed at a later date). Kagome and pyrochlore are also popular models within my community. The shuriken lattice is more uncommon, but gaining ground in the frustration community.

Shurikens

Japanese Shurikens- a type of ninja fighting star. _{By kaex0r (http://www.flickr.com/photos/kaex0r414/191765028/) [CC BY 2.0 (http://creativecommons.org/licenses/by/2.0)], via Wikimedia Commons}

# importing our packages
Pkg.add("PyPlot");
Pkg.update();
using PyPlot;

lattice="shuriken";

Nx=3;
Ny=3;
Nz=1;

# A cell to just evaluate
# This one sets the unit vectors (a,b,c) for the different unit cells
# Can you guess what a lattice will look like by looking at the vectors?
if(lattice=="honeycomb") #also the graphite lattice
    d=2;
    Ncell=2;
    unit=[[0 0 0]
        [sqrt(3)/2 1/2 0]];
    a=[sqrt(3),0,0];
    b=[sqrt(3)/2,3/2,0];
    c=[0,0,1];
elseif(lattice=="kagome")
    d=2;
    Ncell=3;
    unit=[[0 0 0]
          [1 0 0]
        [.5 sqrt(3)/2 0]];
    a=[2,0,0];       #Look familiar? Checkout pt from Pt. 1
    b=[1, sqrt(3), 0];
    c=[0,0,1];
elseif(lattice=="shuriken")
    d=2;
    Ncell=6;
    unit=[[0 0 0]
          [.5 0 0]
          [0 .5 0]
          [.5 .5 0]
        [.5+.25*sqrt(3) .25 0]
        [.25 .5+.25*sqrt(3) 0]];
    a=[.5+.5*sqrt(3),0,0];
    b=[0,.5+.5*sqrt(3),0];
    c=[0,0,1];
elseif(lattice=="diamond")
    d=3;
    Ncell=2;
    unit=[[0 0 0]
          [.25 .25 .25]];
    a=[.5,.5,0];    #Look familiar? Checkout fcc from Pt.1
    b=[.5,0,.5];
    c=[0,.5,.5];
elseif(lattice=="pyrochlore")
    d=3;
    Ncell=4;
    unit=[[0 0 0]
        [.25 .25 0]
        [.25 0 .25]
        [0 .25 .25]];
    a=[.5,.5,0];
    b=[.5,0,.5];
    c=[0,.5,.5];

else
    println("Please have a correct lattice")
end
"Cell finished"

Connections to Bravais Lattices

If you look at some of the comments above, and checkout the basis vectors from Crystal Shapes, like pt,
begin{equation}
a=[1,0,0];;;;;;;;; b=[.5,frac{sqrt{3}}{2},0],
end{equation}
you’ll notice they’re the same except for a scaling factor. This has to be true, since only 14 different patterns tile 3D space uniquely.

# Another cell to just evaluate
# Here we set up some numbers and matrices for our computation
N=Nx*Ny*Nz*Ncell;    #The total number of sites
aM=transpose(repeat(a,outer=[1,Ncell]));
bM=transpose(repeat(b,outer=[1,Ncell*Nx])); #these allow us to copy an entire row or layer at once
cM=transpose(repeat(c,outer=[1,Ncell*Nx*Ny]));

X=Array{Float64}(N,3);  #where we store the positions
"Cell finished"

# Another cell to just evaluate
# Here we are actually calculating the positions for every site
for i in 1:Nx    #for the first row
    X[Ncell*i-Ncell+1:Ncell*i,:]=unit+(i-1)*aM;
end

for j in 2:Ny    #copying the first row into the first layer
    X[Ncell*Nx*(j-1)+(1:Ncell*Nx),:]=X[1:Ncell*Nx,:]+(j-1)*bM;
end

for j in 2:Nz    #copying the first layer into the entire cube
    X[Ncell*Ny*Nx*(j-1)+(1:Ncell*Nx*Ny),:]=X[1:Ncell*Nx*Ny,:]+(j-1)*cM;
end
"Cell finished"

# 2D plotter
pygui(false)
w, h = plt[:figaspect](1)
figure(figsize=(w,h))
scatter(X[:,1],X[:,2])

Shuriken

3×3 Shuriken or Square-Kagome Lattice.

# 3D plotter
pygui(false)
w, h = plt[:figaspect](1)
figure(figsize=(w,h))
areas=100*ones(length(X[:,1]))
scatter3D(X[:,1],X[:,2],X[:,3])

Perdy Pictures

From these plots, some 3D structures like the pyrochlore are hard to visualize. So here’s a nice graphic I made that might help a little bit more.

Pyrochlore

Hopefully this pyrochlore is a little easier to visualize than the pyplot version. Took me long enough to make in inkscape.

honeycomb

Tikz produced Honeycomb. Coloring indicative of the lattice description of the Kitaev model.

The honeycomb, like several other lattices you see around here, is bipartite.
You can see in my image that black sites are only next to white sites, and vice versa.
This property can make the system much easier to work with. What lattices are bipartite, and which ones aren’t?

If you keep reading, these lattices will keep cropping up again and again. I’ll probably throw in some new ones as well.

Anyway, we will move onto some Quantum Mechanics to look at atomic orbitals soon!

juliabloggers.com

A Julia Language Blog Aggregator

Tag Archives: General

Data Wrangling in Julia based on dplyr Flights Tutorials

Data

Load packages and example dataset

@where: Keep rows matching criteria

@select: Pick columns by name

“Chaining” or “Pipelining”

@orderby: Reorder rows

@transform: Add new variables

@by: Reduce variables to values (Grouping and Summarizing)

Other useful convenience functions

Conclusion

Computationally Visualizing Crystals

Christina C. Lee, github: albi3ro

Define The Relevant Variables

Programming Tip:

Go Back and Fiddle!

Computationally Visualizing Crystals Pt. 2

Christina C. Lee, github: albi3ro

Introducing Some Lattice Options

Connections to Bravais Lattices

Perdy Pictures