By: Bradley Setzler

Re-posted from: http://juliaeconomics.com/2014/06/16/bootstrapping-and-hypothesis-tests-in-julia/

* The script to reproduce the results of this tutorial in Julia is located here.

Suppose that we wish to test to see if the the parameter estimates of 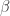are statistically different from zero and if the estimate of 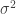is different from one for the OLS parameters defined in a previous post. Suppose further that we do not know how to compute analytically the standard errors of the MLE parameter estimates; the MLE estimates were presented in the most recent post.

We decide to bootstrap by resampling cases in order to estimate the standard errors. This means that we treat the sample of 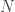individuals as if it were a population from which we randomly draw 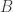subsamples, each of size 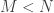. This produces a sample of MLEs of size 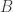, that is, it provides an empirical approximation to the distribution of the MLEs. From the empirical approximation, we can compare the full-sample point MLE to the MLE distribution under the null hypothesis.

Unfortunately, Julia does not have built-in bootstrapping yet, but I found a way to do it in one line with the randperm function.

---

Wrapper Functions and the Likelihood of Interest

Now that we have a bootstrap index, we define the log-likelihood as a function of x and y, which are any subsets of X and Y, respectively.

function loglike(rho,y,x)
   beta = rho[1:4]
   sigma2 = exp(rho[5])
   residual = y-*(x,beta)
   dist = Normal(0, sigma2)
   contributions = logpdf(dist,residual)
   loglikelihood = sum(contributions)
   return -loglikelihood
end

Then, if we wish to evaluate loglike across various subsets of x and y, we use what is called a wrapper, which simply creates a copy of loglike that has already set the values of x and y. For example, the following function will evaluate loglike when x=X and y=Y:

function wrapLoglike(rho)
   return loglike(rho,Y,X)
end

We do this because we want the optimizer to find the optimal 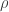, holding x and y fixed, but we also want to be able to adjust x and y to suit our purposes. The wrapper function allows the user to modify x and y, but tells the optimizer not to mess with them.

Tip: Use wrapper functions to manage arguments of your objective function that are not supposed to be accessed by the optimizer. Give the optimizer functions with only one argument — the parameters over which it is supposed to optimize your objective function.

---

Bootstrapping the OLS MLE

Now, we will use a random index, which I created from the randperm function, to take a random subset of individuals from the data, feed them into the function using a wrapper, then have the optimizer maximize the wrapper across the parameters. We repeat this process in a loop, so that we obtain the MLE for each subset. The following loop stores the MLE in each row of the matrix samples using 1,000 bootstrap samples of size one-half (M) of the available sample:

M=convert(Int,N/2)
B=1000
samples = zeros(B,5)
for b=1:B
   theIndex = randperm(N)[1:M]
   x = X[theIndex,:]
   y = Y[theIndex,:]
   function wrapLoglike(rho)
      return loglike(rho,y,x)
   end
   samples[b,:] = optimize(wrapLoglike,params0,method=:cg).minimum
end
samples[:,5] = exp(samples[:,5])

The resulting matrix contains 1,000 samples of the MLE. As always, we must remember to exponentiate the variance estimates, because they were stored in log-units.

---

Bootstrapping for Non-parametric p-values

Estimates of the standard errors of the MLE estimates can be obtained by computing the standard deviation of each column,

bootstrapSE = std(samples,1)

where the number 1 indicates that the standard deviation is taken over columns (instead of rows).

Standard errors like these can be used directly for hypothesis testing under parametric assumptions. For example, if we assume an MLE is normally distributed, then we reject the null hypothesis that the parameter is equal to some point if the parameter estimate differs from the point by at least 1.96 standard errors (using that the sample is large). However, we can make fewer assumptions using non-parametric p-values. 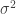The following code creates the distribution implied by the null hypothesis that by subtracting the mean from each distribution (thus imposing a zero mean) and then adding 1 to the distribution of (thus imposing a mean of one); this is called nullDistribution.

nullDistribution = samples
pvalues = ones(5)
for i=1:5
   nullDistribution[:,i] = nullDistribution[:,i]-mean(nullDistribution[:,i])
end
nullDistribution[:,5] = 1 + nullDistribution[:,5]

The non-parametric p-value (for two-sided hypothesis testing) is the fraction of times that the absolute value of the MLE is greater than the absolute value of the null distribution.

pvalues = [mean(abs(MLE[i]).<abs(nullDistribution[:,i])) for i=1:5]

If we are interested in one-sided hypothesis testing, the following code would test the null hypothesis 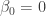against the alternative that :

pvalues = [mean(MLE[i].<nullDistribution[:,i]) for i=1:5]

Conversely, the following code would test the null hypothesis 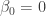against the alternative that :

pvalues = [mean(MLE[i].>nullDistribution[:,i]) for i=1:5]

Thus, two-sided testing uses the absolute value (abs), and one-sided testing only requires that we choose the right comparison operator (.> or .<).

---

Results

The resulting bootstrap standard errors are,

julia> bootstrapSE
1x5 Array{Float64,2}:
0.0316747 0.0312018 0.0327237 0.0306751 0.0208552

and the non-parametric two-sided p-value estimates are,

julia> pvalues
5-element Array{Any,1}:
0.001
0.0
0.0
0.727
0.305

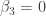Thus, we reject the null hypotheses for the first three parameters and conclude that , but find insufficient evidence to reject the null hypotheses that  and 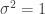. Comparing these conclusions to trueParams, we see that the non-parametric p-values performed well.

---

Bradley J. Setzler