Re-posted from: http://www.stochasticlifestyle.com/solving-systems-stochastic-pdes-using-gpus-julia/
What I want to describe in this post is how to solve stochastic PDEs in Julia using GPU parallelism. I will go from start to finish, describing how to use the type-genericness of the DifferentialEquations.jl library in order to write a code that uses within-method GPU-parallelism on the system of PDEs. This is mostly a proof of concept: the most efficient integrators for this problem are not compatible with GPU parallelism yet, and the GPU parallelism isn’t fully efficient yet. However, I thought it would be nice to show an early progress report showing that it works and what needs to be fixed in Base Julia and various libraries for us to get the full efficiency.
Our Problem: 2-dimensional Reaction-Diffusion Equations
The reaction-diffusion equation is a PDE commonly handled in systems biology which is a diffusion equation plus a nonlinear reaction term. The dynamics are defined as:

But this doesn’t need to only have a single “reactant” u: this can be a vector of reactants and the  is then the nonlinear vector equations describing how these different pieces react together. Let’s settle on a specific equation to make this easier to explain. Let’s use a simple model of a 3-component system where A can diffuse through space to bind with the non-diffusive B to form the complex C (also non-diffusive, assume B is too big and gets stuck in a cell which causes C=A+B to be stuck as well). Other than the binding, we make each of these undergo a simple birth-death process, and we write down the equations which result from mass-action kinetics. If this all is meaningless to you, just understand that it gives the system of PDEs:
is then the nonlinear vector equations describing how these different pieces react together. Let’s settle on a specific equation to make this easier to explain. Let’s use a simple model of a 3-component system where A can diffuse through space to bind with the non-diffusive B to form the complex C (also non-diffusive, assume B is too big and gets stuck in a cell which causes C=A+B to be stuck as well). Other than the binding, we make each of these undergo a simple birth-death process, and we write down the equations which result from mass-action kinetics. If this all is meaningless to you, just understand that it gives the system of PDEs:
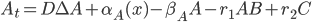

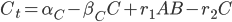
One addition that was made to the model is that we let  be the production of
be the production of  , and we let that be a function of space so that way it only is produced on one side of our equation. Let’s make it a constant when x>80, and 0 otherwise, and let our spatial domain be
, and we let that be a function of space so that way it only is produced on one side of our equation. Let’s make it a constant when x>80, and 0 otherwise, and let our spatial domain be ![x \in [0,100]](https://i2.wp.com/www.stochasticlifestyle.com/wp-content/plugins/latex/cache/tex_944e326e3dddc5dae1278b292b330d64.gif) and
and ![y \in [0,100]](https://i1.wp.com/www.stochasticlifestyle.com/wp-content/plugins/latex/cache/tex_43a28f59556b8f63f126a3ebe74b69ae.gif) .
.
This model is spatial: each reactant 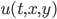 is defined at each point in space, and all of the reactions are local, meaning that
is defined at each point in space, and all of the reactions are local, meaning that  at spatial point
at spatial point  only uses
only uses 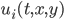 . This is an important fact which will come up later for parallelization.
. This is an important fact which will come up later for parallelization.
Discretizing the PDE into ODEs
In order to solve this via a method of lines (MOL) approach, we need to discretize the PDE into a system of ODEs. Let’s do a simple uniformly-spaced grid finite difference discretization. Choose  and
and  so that we have 100*100=10000 points for each reactant. Notice how fast that grows! Put the reactants in a matrix such that A[i,j] =
so that we have 100*100=10000 points for each reactant. Notice how fast that grows! Put the reactants in a matrix such that A[i,j] =  , i.e. the columns of the matrix is the
, i.e. the columns of the matrix is the  values and the rows are the
values and the rows are the  values (this way looking at the matrix is essentially like looking at the discretized space).
values (this way looking at the matrix is essentially like looking at the discretized space).
So now we have 3 matrices (A, B, and C) for our reactants. How do we discretize the PDE? In this case, the diffusion term simply becomes a tridiagonal matrix  where
where ![[1,-2,1]](https://i0.wp.com/www.stochasticlifestyle.com/wp-content/plugins/latex/cache/tex_524fb89308e20bfe4e3ce99ffee459a6.gif) is central band. You can notice that
is central band. You can notice that  performs diffusion along the columns of
performs diffusion along the columns of  , and so this is diffusion along the
, and so this is diffusion along the  . Similarly,
. Similarly,  flips the indices and thus does diffusion along the rows of
flips the indices and thus does diffusion along the rows of  making this diffusion along
making this diffusion along  . Thus
. Thus  is the discretized Laplacian (we could have separate diffusion constants and
is the discretized Laplacian (we could have separate diffusion constants and  if we want by using different constants on the
if we want by using different constants on the  , but let’s not do that for this simple example. I’ll leave that as an exercise for the reader). I enforced a Neumann boundary condition with zero derivative (also known as a no-flux boundary condition) by reflecting the changes over the boundary. Thus the derivative operator is generated as:
, but let’s not do that for this simple example. I’ll leave that as an exercise for the reader). I enforced a Neumann boundary condition with zero derivative (also known as a no-flux boundary condition) by reflecting the changes over the boundary. Thus the derivative operator is generated as:
const Mx = full(Tridiagonal([1.0 for i in 1:N-1],[-2.0 for i in 1:N],[1.0 for i in 1:N-1])) const My = copy(Mx) # Do the reflections, different for x and y operators Mx[2,1] = 2.0 Mx[end-1,end] = 2.0 My[1,2] = 2.0 My[end,end-1] = 2.0
I also could have done this using the DiffEqOperators.jl library, but I wanted to show what it truly is at its core.
Since all of the reactions are local, we only have each point in space react separately. Thus this represents itself as element-wise equations on the reactants. Thus we can write it out quite simply. The ODE which then represents the PDE is thus in pseudo Julia code:
DA = D*(M*A + A*M) @. DA + α₁ - β₁*A - r₁*A*B + r₂*C @. α₂ - β₂*B - r₁*A*B + r₂*C @. α₃ - β₃*C + r₁*A*B - r₂*C
Note here that I am using α₁ as a matrix (or row-vector, since that will broadcast just fine) where every point in space with x<80 has this zero, and all of the others have it as a constant. The other coefficients are all scalars. How do we do this with the ODE solver?
Our Type: ArrayPartition
The ArrayPartition is an interesting type from RecursiveArrayTools.jl which allows you to define “an array” as actually being different discrete subunits of arrays. Let’s assume that our initial condition is zero for everything and let the production terms build it up. This means that we can define:
A = zeros(M,N); B = zeros(M,N); C = zeros(M,N)
Now we can put them together as:
u0 = ArrayPartition((A,B,C))
You can read the RecursiveArrayTools.jl README to get more familiar with what the ArrayPartition is, but really it’s an array where u[i] indexes into A first, B second, then C. It also has efficient broadcast, doing the A, B and C parts together (and this is efficient even if they don’t match types!). But since this acts as an array, to DifferentialEquations.jl it is an array!
The important part is that we can “decouple” the pieces of the array at anytime by accessing u.x, which holds our tuple of arrays. Thus our ODE using this ArrayPartition as its container can be written as follows:
function f(t,u,du) A,B,C = u.x dA,dB,dC = du.x DA = D*(M*A + A*M) @. dA = DA + α₁ - β₁*A - r₁*A*B + r₂*C @. dB = α₂ - β₂*B - r₁*A*B + r₂*C @. dC = α₃ - β₃*C + r₁*A*B - r₂*C end
where this is using @. to do inplace updates on our du to say how the full ArrayPartition should update in time. Note that we can make this more efficient by adding some cache variables to the diffusion matrix multiplications and using A_mul_B!, but let’s ignore that for now.
Together, the ODE which defines our PDE is thus:
prob = ODEProblem(f,u0,(0.0,100.0)) sol = solve(prob,BS3())
if I want to solve it on ![t \in [0,100]](https://i1.wp.com/www.stochasticlifestyle.com/wp-content/plugins/latex/cache/tex_e30a2ff606c68b20c3adbcdc6c97f8a3.gif) . Done! The solution gives back ArrayPartitions (and interpolates to create new ones if you use sol(t)). We can plot it in Plots.jl
. Done! The solution gives back ArrayPartitions (and interpolates to create new ones if you use sol(t)). We can plot it in Plots.jl

and see the pretty gradients. Using this 3rd order explicit adaptive Runge-Kutta method we solve this equation in about 40 seconds. That’s okay.
Some Optimizations
There are some optimizations that can still be done. When we do A*B as matrix multiplication, we create another temporary matrix. These allocations can bog down the system. Instead we can pre-allocate the outputs and use the inplace functions A_mul_B! to make better use of memory. The easiest way to store these cache arrays are constant globals, but you can use closures (anonymous functions which capture data, i.e. (x)->f(x,y)) or call-overloaded types to do it without globals. The globals way (the easy way) is simply:
const MyA = zeros(N,N) const AMx = zeros(N,N) const DA = zeros(N,N) function f(t,u,du) A,B,C = u.x dA,dB,dC = du.x A_mul_B!(MyA,My,A) A_mul_B!(AMx,A,Mx) @. DA = D*(MyA + AMx) @. dA = DA + α₁ - β₁*A - r₁*A*B + r₂*C @. dB = α₂ - β₂*B - r₁*A*B + r₂*C @. dC = α₃ - β₃*C + r₁*A*B - r₂*C end
For reference, closures looks like:
MyA = zeros(N,N) AMx = zeros(N,N) DA = zeros(N,N) function f_full(t,u,du,MyA,AMx,DA) A,B,C = u.x dA,dB,dC = du.x A_mul_B!(MyA,My,A) A_mul_B!(AMx,A,Mx) @. DA = D*(MyA + AMx) @. dA = DA + α₁ - β₁*A - r₁*A*B + r₂*C @. dB = α₂ - β₂*B - r₁*A*B + r₂*C @. dC = α₃ - β₃*C + r₁*A*B - r₂*C end f = (t,u,du)-> f_full(t,u,du,MyA,AMx,DA)
and a call overloaded type looks like:
struct MyFunction{T} <: Function
MyA::T
AMx::T
DA::T
end
# Now define the overload
function (ff::MyFunction)(t,u,du)
# This is a function which references itself via ff
A,B,C = u.x
dA,dB,dC = du.x
A_mul_B!(ff.MyA,My,A)
A_mul_B!(ff.AMx,A,Mx)
@. ff.DA = D*(ff.MyA + ff.AMx)
@. dA = f.DA + α₁ - β₁*A - r₁*A*B + r₂*C
@. dB = α₂ - β₂*B - r₁*A*B + r₂*C
@. dC = α₃ - β₃*C + r₁*A*B - r₂*C
end
MyA = zeros(N,N)
AMx = zeros(N,N)
DA = zeros(N,N)
f = MyFunction(MyA,AMx,DA)
# Now f(t,u,du) is our function!
These last two ways enclose the pointer to our cache arrays locally but still present a function f(t,u,du) to the ODE solver.
Now since PDEs are large, many times we don’t care about getting the whole timeseries. Using the output controls from DifferentialEquations.jl, we can make it only output the final timepoint.
sol = solve(prob,BS3(),progress=true,save_everystep=false,save_start=false)
Also, if you’re using Juno this’ll give you a nice progress bar so you can track how it’s going.
Quick Note About Performance
We are using an explicit Runge-Kutta method here because that’s what works with GPUs so far. Matrix factorizations need to be implemented for GPUArrays before the implicit (stiff) solvers will be available, so here we choose BS3 since it’s fully broadcasting (not all methods are yet) and it’s fully GPU compatible. In practice, right now using an NxNx3 tensor as the initial condition / dependent variable with either OrdinaryDiffEq’s Rosenbrock23(), Rodas4(), or Sundials’ CVODE_BDF() is actually more efficient right now. But after Julia fixes its broadcasting issue and with some updates to Julia’s differentiation libraries to handle abstract arrays like in DiffEqDiffTools.jl, the stiff solvers will be usable with GPUs and all will be well.
Thus for reference I will show some ways to do this efficiently with stiff solvers. With a stiff solver we will not want to factorize the dense Jacobian since that would take forever. Instead we can use something like Sundials’ Krylov method:
u0 = zeros(N,N,3) const MyA = zeros(N,N); const AMx = zeros(N,N); const DA = zeros(N,N) function f(t,u,du) A = @view u[:,:,1] B = @view u[:,:,2] C = @view u[:,:,3] dA = @view du[:,:,1] dB = @view du[:,:,2] dC = @view du[:,:,3] A_mul_B!(MyA,My,A) A_mul_B!(AMx,A,Mx) @. DA = D*(MyA + AMx) @. dA = DA + α₁ - β₁*A - r₁*A*B + r₂*C @. dB = α₂ - β₂*B - r₁*A*B + r₂*C @. dC = α₃ - β₃*C + r₁*A*B - r₂*C end # Solve the ODE prob = ODEProblem(f,u0,(0.0,100.0)) using Sundials @time sol = solve(prob,CVODE_BDF(linear_solver=:BCG))
and that will solve it in about a second. In this case it wouldn’t be more efficient to use the banded linear solver since the system of equations tends to have different parts of the system interact which makes the bands large, and thus a Krylov method is preferred. See this part of the docs for details on the available linear solvers from Sundials. DifferentialEquations.jl exposes a ton of Sundials’ possible choices so hopefully one works for your problem (preconditioners coming soon).
To do something similar with OrdinaryDiffEq.jl, we would need to make use of the linear solver choices in order to override the internal linear solve functions with some kind of sparse matrix solver like a Krylov method from IterativeSolvers.jl. For this size of problem though a multistep method like BDF is probably preferred though, at least until we implement some IMEX methods.
So if you want to solve it quickly right now, that’s how you do it. But let’s get back to our other story: the future is more exciting.
The Full ODE Code
As a summary, here’s a full PDE code:
using OrdinaryDiffEq, RecursiveArrayTools # Define the constants for the PDE const α₂ = 1.0 const α₃ = 1.0 const β₁ = 1.0 const β₂ = 1.0 const β₃ = 1.0 const r₁ = 1.0 const r₂ = 1.0 const D = 100.0 const γ₁ = 0.1 const γ₂ = 0.1 const γ₃ = 0.1 const N = 100 const X = reshape([i for i in 1:100 for j in 1:100],N,N) const Y = reshape([j for i in 1:100 for j in 1:100],N,N) const α₁ = 1.0.*(X.>=80) const Mx = full(Tridiagonal([1.0 for i in 1:N-1],[-2.0 for i in 1:N],[1.0 for i in 1:N-1])) const My = copy(Mx) Mx[2,1] = 2.0 Mx[end-1,end] = 2.0 My[1,2] = 2.0 My[end,end-1] = 2.0 # Define the initial condition as normal arrays A = zeros(N,N); B = zeros(N,N); C = zeros(N,N) u0 = ArrayPartition((A,B,C)) const MyA = zeros(N,N); const AMx = zeros(N,N); const DA = zeros(N,N) # Define the discretized PDE as an ODE function function f(t,u,du) A,B,C = u.x dA,dB,dC = du.x A_mul_B!(MyA,My,A) A_mul_B!(AMx,A,Mx) @. DA = D*(MyA + AMx) @. dA = DA + α₁ - β₁*A - r₁*A*B + r₂*C @. dB = α₂ - β₂*B - r₁*A*B + r₂*C @. dC = α₃ - β₃*C + r₁*A*B - r₂*C end # Solve the ODE prob = ODEProblem(f,u0,(0.0,100.0)) sol = solve(prob,BS3(),progress=true,save_everystep=false,save_start=false) using Plots; pyplot() p1 = surface(X,Y,sol[end].x[1],title = "[A]") p2 = surface(X,Y,sol[end].x[2],title = "[B]") p3 = surface(X,Y,sol[end].x[3],title = "[C]") plot(p1,p2,p3,layout=grid(3,1))
Making Use of GPU Parallelism
That was all using the CPU. How do we make turn on GPU parallelism with DifferentialEquations.jl? Well, you don’t. DifferentialEquations.jl “doesn’t have GPU bits”. So wait… can we not do GPU parallelism? No, this is the glory of type-genericness, especially in broadcasted operations. To make things use the GPU, we simply use a GPUArray. If instead of zeros(N,M) we used GPUArray(zeros(N,M)), then u becomes an ArrayPartition of GPUArrays. GPUArrays naturally override broadcast such that dotted operations are performed on the GPU. DifferentialEquations.jl uses broadcast internally (except in this list of current exceptions due to a limitation with Julia’s inference engine which I have discussed with Jameson Nash (@vtjnash) who mentioned this should be fixed in Julia’s 1.0 release), and thus just by putting the array as a GPUArray, the array-type will take over how all internal updates are performed and turn this algorithm into a fully GPU-parallelized algorithm that doesn’t require copying to the CPU. Wasn’t that simple?
From that you can probably also see how to multithread everything, or how to set everything up with distributed parallelism. You can make the ODE solvers do whatever you want by defining an array type where the broadcast does whatever special behavior you want.
So to recap, the entire difference from above is changing to:
using CLArrays gA = CLArray(A); gB = CLArray(B); gC = CLArray(C) const gMx = CLArray(Mx) const gMy = CLArray(My) const gα₁ = CLArray(α₁) gu0 = ArrayPartition((gA,gB,gC)) const gMyA = zeros(N,N) const gAMx = zeros(N,N) const gDA = zeros(N,N) function gf(t,u,du) A,B,C = u.x dA,dB,dC = du.x A_mul_B!(gMyA,gMy,A) A_mul_B!(gAMx,A,gMx) @. DA = D*(gMyA + AgMx) @. dA = DA + gα₁ - β₁*A - r₁*A*B + r₂*C @. dB = α₂ - β₂*B - r₁*A*B + r₂*C @. dC = α₃ - β₃*C + r₁*A*B - r₂*C end prob2 = ODEProblem(gf,gu0,(0.0,100.0)) GPUArrays.allowslow(false) # makes sure none of the slow fallbacks are used @time sol = solve(prob2,BS3(),progress=true,dt=0.003,adaptive=false,save_everystep=false,save_start=false) prob2 = ODEProblem(gf,gu0,(0.0,100.0)) sol = solve(prob2,BS3(),progress=true,save_everystep=false,save_start=false) # Adaptivity currently fails due to https://github.com/JuliaGPU/CLArrays.jl/issues/10
You can use CUArrays if you want as well. It looks exactly the same as using CLArrays except you exchange the CLArray calls to CUArray. Go have fun.
And Stochastic PDEs?
Why not make it an SPDE? All that we need to do is extend each of the PDE equations to have a noise function. In this case, let’s use multiplicative noise on each reactant. This means that our noise update equation is:
function g(t,u,du) A,B,C = u.x dA,dB,dC = du.x @. dA = γ₁*A @. dB = γ₂*A @. dC = γ₃*A end
Now we just define and solve the system of SDEs:
prob = SDEProblem(f,g,u0,(0.0,100.0)) sol = solve(prob,SRIW1())

We can see the cool effect that diffusion dampens the noise in [A] but is unable to dampen the noise in [B] which results in a very noisy [C]. The stiff SPDE takes much longer to solve even using high order plus adaptivity because stochastic problems are just that much more difficult (current research topic is to make new algorithms for this!). It gets GPU’d just by using GPUArrays like before. But there we go: solving systems of stochastic PDEs using high order adaptive algorithms with within-method GPU parallelism. That’s gotta be a first? The cool thing is that nobody ever had to implement the GPU-parallelism either, it just exists by virtue of the Julia type system.
Side Notes
Warning: This can take awhile to solve! An explicit Runge-Kutta algorithm isn’t necessarily great here, though to use a stiff solver on a problem of this size requires once again smartly choosing sparse linear solvers. The high order adaptive method is pretty much necessary though since something like Euler-Maruyama is simply not stable enough to solve this at a reasonable dt. Also, the current algorithms are not so great at handling this problem. Good thing there’s a publication coming along with some new stuff…
Note: the version of SRIW1 which uses broadcast for GPUs is not on the current versions of StochasticDiffEq.jl since it’s slower due to a bug when fusing too many broadcasts which will hopefully get fixed in one of Julia’s 1.x releases. Until then, GPUs cannot be used with this algorithm without a (quick) modification.
Conclusion
So that’s where we’re at. GPU parallelism works because of abstract typing. But in some cases we need to help the GPU array libraries get up to snuff to handle all of the operations, and then we’ll really be in business! Of course there’s more optimizing that needs to be done, and we can do this by specializing code paths on bottlenecks as needed.
I think this is at least a nice proof of concept showing that Julia’s generic algorithms allow for one to not only take advantage of things like higher precision, but also take advantage of parallelism and extra hardware without having to re-write the underlying algorithm. There’s definitely more work that needs to be done, but I can see this usage of abstract array typing as being one of Julia’s “killer features” in the coming years as the GPU community refines its tools. I’d give at least a year before all of this GPU stuff is compatible with stiff solvers and linear solver choices (so that way it can make use of GPU-based Jacobian factorizations and Krylov methods). And comparable methods for SDEs are something I hope to publish soon since the current tools are simply not fit for this scale of problem: high order, adaptivity, sparse linear solvers, and A/L-stability all need to be combined in order to tackle this problem efficiently.
Full Script
Here’s the full script for recreating everything:
####################################################### ### Solve the PDE ####################################################### using OrdinaryDiffEq, RecursiveArrayTools # Define the constants for the PDE const α₂ = 1.0 const α₃ = 1.0 const β₁ = 1.0 const β₂ = 1.0 const β₃ = 1.0 const r₁ = 1.0 const r₂ = 1.0 const D = 100.0 const γ₁ = 0.1 const γ₂ = 0.1 const γ₃ = 0.1 const N = 100 const X = reshape([i for i in 1:100 for j in 1:100],N,N) const Y = reshape([j for i in 1:100 for j in 1:100],N,N) const α₁ = 1.0.*(X.>=80) const Mx = full(Tridiagonal([1.0 for i in 1:N-1],[-2.0 for i in 1:N],[1.0 for i in 1:N-1])) const My = copy(Mx) Mx[2,1] = 2.0 Mx[end-1,end] = 2.0 My[1,2] = 2.0 My[end,end-1] = 2.0 # Define the initial condition as normal arrays A = zeros(N,N); B = zeros(N,N); C = zeros(N,N) u0 = ArrayPartition((A,B,C)) const MyA = zeros(N,N); const AMx = zeros(N,N); const DA = zeros(N,N) # Define the discretized PDE as an ODE function function f(t,u,du) A,B,C = u.x dA,dB,dC = du.x A_mul_B!(MyA,My,A) A_mul_B!(AMx,A,Mx) @. DA = D*(MyA + AMx) @. dA = DA + α₁ - β₁*A - r₁*A*B + r₂*C @. dB = α₂ - β₂*B - r₁*A*B + r₂*C @. dC = α₃ - β₃*C + r₁*A*B - r₂*C end # Solve the ODE prob = ODEProblem(f,u0,(0.0,100.0)) @time sol = solve(prob,BS3(),progress=true,save_everystep=false,save_start=false) using Plots; pyplot() p1 = surface(X,Y,sol[end].x[1],title = "[A]") p2 = surface(X,Y,sol[end].x[2],title = "[B]") p3 = surface(X,Y,sol[end].x[3],title = "[C]") plot(p1,p2,p3,layout=grid(3,1)) ####################################################### ### Solve the PDE using CLArrays ####################################################### using CLArrays gA = CLArray(A); gB = CLArray(B); gC = CLArray(C) const gMx = CLArray(Mx) const gMy = CLArray(My) const gα₁ = CLArray(α₁) gu0 = ArrayPartition((gA,gB,gC)) const gMyA = CLArray(MyA) const gAMx = CLArray(AMx) const gDA = CLArray(DA) function gf(t,u,du) A,B,C = u.x dA,dB,dC = du.x A_mul_B!(gMyA,gMy,A) A_mul_B!(gAMx,A,gMx) @. gDA = D*(gMyA + gAMx) @. dA = gDA + gα₁ - β₁*A - r₁*A*B + r₂*C @. dB = α₂ - β₂*B - r₁*A*B + r₂*C @. dC = α₃ - β₃*C + r₁*A*B - r₂*C end prob2 = ODEProblem(gf,gu0,(0.0,100.0)) GPUArrays.allowslow(false) @time sol = solve(prob2,BS3(),progress=true,dt=0.003,adaptive=false,save_everystep=false,save_start=false) prob2 = ODEProblem(gf,gu0,(0.0,100.0)) sol = solve(prob2,BS3(),progress=true,save_everystep=false,save_start=false) # Adaptivity currently fails due to https://github.com/JuliaGPU/CLArrays.jl/issues/10 ####################################################### ### Solve the SPDE ####################################################### using StochasticDiffEq function g(t,u,du) A,B,C = u.x dA,dB,dC = du.x @. dA = γ₁*A @. dB = γ₂*A @. dC = γ₃*A end prob3 = SDEProblem(f,g,u0,(0.0,100.0)) sol = solve(prob3,SRIW1(),progress=true,save_everystep=false,save_start=false) p1 = surface(X,Y,sol[end].x[1],title = "[A]") p2 = surface(X,Y,sol[end].x[2],title = "[B]") p3 = surface(X,Y,sol[end].x[3],title = "[C]") plot(p1,p2,p3,layout=grid(3,1)) # Exercise: Do SPDE + GPU
The post Solving Systems of Stochastic PDEs and using GPUs in Julia appeared first on Stochastic Lifestyle.
 ).
).

