By: Jacob Quinn
Re-posted from: https://quinnj.home.blog/2019/06/20/generated-constant-propagation-hold-on-to-your-britches/
In a recent JuliaLang Discourse post, OP was looking for a simple way to convert their Vector{CustomType} to a DataFrame, treating each CustomType element as a “row”, with the fields of CustomType as fields in the row. The post piqued my interest, given my work on the Tables.jl interface over the last year. Tables.jl is geared specifically towards creating generic access patterns to “table” like sources, specifically providing Tables.rows and Tables.columns as two ways to access table data from any source. Tables.columns returns a “property-accessible object” of iterators, while Tables.rows returns the dual: an iterator of “property-accessible objects” (property-accessible object here is defined as any object that supports both propertynames(obj) and getproperty(obj, prop), which includes all custom structs by default).
I decided to respond by showing how simple it can be to “hook in” to the Tables.jl world of interop; my code looked like:
using DataFrames, Random, Tables
struct Mine
a::Int
b::Float64
c::Matrix{Float64}
end
Tables.istable(::Type{Vector{Mine}}) = true
Tables.rowaccess(::Type{Vector{Mine}}) = true
Tables.rows(x::Vector{Mine}) = x
Tables.schema(x::Vector{Mine}) = Tables.Schema((:a, :b), Tuple{Int, Float64})
Random.seed!(999)
v = [Mine(rand(1:10), rand(), rand(2,2)) for i ∈ 1:10^6];
df = DataFrame(v)
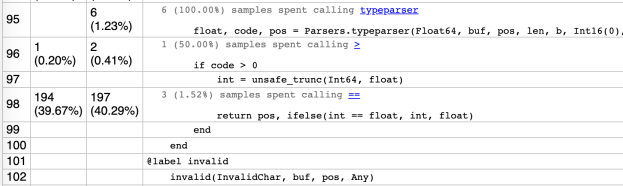
But when doing a quick benchmark of the conversion from Vector{Mine} to DataFrame, it was 3x-5x slower than other methods already proposed. Huh? I started digging. One thing I noticed was by ***not*** defining Tables.schema, the code was a bit faster! That led me to assume something was up in our schema-based row-to-column code.
Part of the challenge with this functionality is wrestling with providing a fast, type-stable method for building up strongly-typed columns for a set of rows with arbitrary number of columns and types. Just iterating over a row in a for-loop, accessing each field programmatically can be disastrous; because each extracted field value in the hot for-loop could be a number of types, the compiler can’t do much more than create a Core.Box to put arbitrary values in, then pull out again for inserting into the vector we’re building up. Yuck, yuck, yuck; if you see Core.Boxs in your @code_typed output, or values inferred as Any, it’s an indication the compiler just couldn’t figure out anything more specific, and in a hot for-loop called over and over and over again, any hope of performance is toast.
Enter meta-programming: Tables.jl tries to judiciously employ the use of @generated functions to help deal w/ the issue here. Specifically, when doing this rows-to-columns conversion, with a known schema, Tables.eachcolumn can take the column names/types as input, and generate a custom function with this aforementioned “hot for-loop” unrolled. That is, instead of:
for rownumber = 1:number_of_rows row = rows[rownumber]
for i = 1:ncols
column[i][rownumber] = getfield(row, i)
endend
For a specific table input’s schema, the generated code looks like:
for rownumber = 1:number_of_rows
row = rows[rownumber]
column[1][rownumber] = getfield(row, 1)
column[2][rownumber] = getfield(row, 2)
# etc.
end
What makes this code ***really*** powerful is the compiler’s ability to do “constant propagation”, which means that, while compiling, when it encounters getfield(row, 1), it can realize, “hey, I know that row is a Mine type, and I see that they’re calling getfield to get the 1 field, and I happen to know that the 1 field of Mine is an Int64, so I’ll throw that information into dataflow analysis so things can get further inlined/optimized”. It’s really the difference between the scenario I described before of the compiler just having to treat the naive for-loop values as Any vs. recognizing that it can figure out the exact types to expect which can make the operation we’re talking about here boil down to a very simple “load”, then “store”, without needing to box/unbox or rely on runtime dynamic dispatch based on types.
Back to the original issue: why was this code slower than the unknown schema case? Well, it turns out that our generated code was actually trying to be clever by calculating a run-length encoding of consecutive types for a schema, then generating mini type-stable for-loops; i.e. the generated code looked like:
for rownumber = 1:number_of_rows
row = rows[rownumber]
# if columns 1 & 2 are Int64
for col = 1:2
column[col][rownumber] = getfield(row, col)
end
# column 3 is a Float64
for col = 3:3
column[col][rownumber] = getfield(row, col)
end
# columns 4 & 5 are Int64 again
for col = 4:5
column[col][rownumber] = getfield(row, col)
end
# etc.
end
While this is clever, and can generate less code when schema types tend to be “sticky” (i.e. lots of the same type consecutively), the problem is in the getfield(row, col) call. Even though the call to each getfield ***should*** be type-stable, as calculated from our run-length encoding, the compiler unfortunately can’t figure that out inside these mini type-stable for-loops. This means no super-inlining/optimizations, so things end up being slower.
So what’s the conclusion here? What can be done? The answer was pretty simple, instead of trying to be extra clever with run-length encodings, if the schema is small enough, just generate the getfield calls directly for each column. The current heuristic is for schemas with less than 100 columns, the code will be generated directly, and for larger schema cases, we’ll try the run-length encoding approach (since it’s still more efficient than the initial naive approach).
Hope you enjoyed a little dive under the hood of Tables.jl and some of the challenges the data ecosystem faces in the powerful type system of Julia. Ping me on twitter with any thoughts or questions.
Cheers.