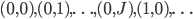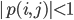Author Archives: Christopher Rackauckas

Multiple-GPU Parallelism on the HPC with Julia

By: Christopher Rackauckas

Re-posted from: http://www.stochasticlifestyle.com/multiple-gpu-on-the-hpc-with-julia/

This is the exciting Part 3 to using Julia on an HPC. First I got you started with using Julia on multiple nodes. Second, I showed you how to get the code running on the GPU. That gets you pretty far. However, if you got a trial allocation on Cometand started running jobs, you may have noticed when looking at the architecture that you’re not getting to use the full GPU. In the job script I showed you, I asked for 2 GPUs. Why? Well, that’s because the flagship NVIDIA GPU, the Tesla K80, is actually a duel GPU and you have to control the two parts separately. You may have been following along on your own computer and have been wondering how you use the multiple GPUs in your setup as well. This tutorial will cover how to extend our function to multiple-GPU setups. You will notice that while this code was made for 2 GPUs, by simply extended the array cudaCores with the values of other GPUs then this code automatically extends to however many you need.

Recall

I want to recall the problem a bit to rephrase it and make it easier to understand why what we are doing will work. Recall that we are simply looping over a mesh of (i,j) (you can think of it as (x,y)) and solving some inner function at each point, and add together the results. The CUDA kernal is shown in the previous part. Thus, how we will extend our problem to multiple GPUs is to simply split the mesh and solve the inner function on different GPUs. It’s critical to realize that this solution method requires independence, i.e. that different parts of the grid do not effect each other. Thus you can think of our function as being a “vectorized” evaluation.

Note that we are not doing the most memory efficient implementation. Each GPU will have the full array of 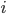i‘s and j‘s even though they will only evaluate it at specific parts. One could split it up, though that would take more work for little performance gain. Thus you should really look into this if you are running low on memory (or to do as an exercise). 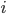If you would like to do this, then you can calculate how far in the i‘s the first GPU calculates, and then only send the right portion of the 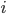i‘s to the other GPU (since we loop down the j‘s, both will need the full j array). Since this problem is not memory limited, I will not show this solution.

Upgrading the Kernal

Upgrading the kernal will be quite simple. Recall that we had the problem in linear indexing before. We will keep the linear indexing, except in each GPU we will pass an integer, StartIdx, which will tell the GPU where in the linear indexing it will start. Thus as before we had the value equalDiv which told the GPU how many indices each core will evaluate, and we had

int index = threadIdx.x + blockIdx.x * blockDim.x;

which tells the GPU which core it is, we have a new global index which is

int globalIndex = index*equalDiv+startIdx;

Notice that each globalIndex is equalDiv apart, and so that is the section each GPU will operate on. The CUDA kernal then just sums up the solution of the inner function over the next equalDiv indices:

    __global__ void integration(const float *coefs, const float *iArr, const float *jArr, const int sizei, const int sizej, const int equalDiv,const int startIdx, int *tmp)
    {
        int index = threadIdx.x + blockIdx.x * blockDim.x;
        int globalIndex = index*equalDiv+startIdx;
        int loopInd;
        float i;
        float j;
        float isq2;
        float isq3;
        float isq4;
        float isq5;
        float isq6;
        float isq7;
        float isq8;
        float jsq2;
        float jsq3;
        float jsq4;
        float jsq5;
        float jsq6;
        float jsq7;
        float jsq8;
        int ans = 0;
        for(loopInd=0;loopInd<equalDiv;loopInd=loopInd+1){
          i = iArr[(globalIndex+loopInd)/sizej];
          j = jArr[(globalIndex+loopInd)%sizej];
          if(globalIndex+loopInd >= sizei*sizej){
            break;
          }
          if((globalIndex+loopInd)%sizej==0 || loopInd==0){
            isq2 = i*i;
            isq3 = i*isq2;
            isq4 = isq2*isq2;
            isq5 = i*isq4;
            isq6 = isq4*isq2;
            isq7 = i*isq6;
            isq8 = isq4*isq4;
          }
          jsq2 = j*j;
          jsq3 = j*jsq2;
          jsq4 = jsq2*jsq2;
          jsq5 = j*jsq4;
          jsq6 = jsq2*jsq4;
          jsq7 = j*jsq6;
          jsq8 = jsq4*jsq4;
          ans = ans + innerFunc(coefs,i,isq2,isq3,isq4,isq5,isq6,isq7,isq8,j,jsq2,jsq3,jsq4,jsq5,jsq6,jsq7,jsq8);
        }
        tmp[index] = ans;
    }

Notice that the inner function did not have to be changed at all:

  __device__ int innerFunc(const float *coefs,const float i,const float isq2,const float isq3,const float isq4,const float isq5,const float isq6,const float isq7,const float isq8,const float j,const float jsq2,const float jsq3,const float jsq4,const float jsq5,const float jsq6,const float jsq7,const float jsq8)
  {
    return abs(coefs[0]*(jsq2) + coefs[1]*(jsq3) + coefs[2]*(jsq4) + coefs[3]*(jsq5) + coefs[4]*jsq6 + coefs[5]*jsq7 + coefs[6]*jsq8 + coefs[7]*(i) + coefs[8]*(i)*(jsq2) + coefs[9]*i*jsq3 + coefs[10]*(i)*(jsq4) + coefs[11]*i*jsq5 + coefs[12]*(i)*(jsq6) + coefs[13]*i*jsq7 + coefs[14]*(isq2) + coefs[15]*(isq2)*(jsq2) + coefs[16]*isq2*jsq3 + coefs[17]*(isq2)*(jsq4) + coefs[18]*isq2*jsq5 + coefs[19]*(isq2)*(jsq6) + coefs[20]*(isq3) + coefs[21]*(isq3)*(jsq2) + coefs[22]*isq3*jsq3 + coefs[23]*(isq3)*(jsq4) + coefs[24]*isq3*jsq5 + coefs[25]*(isq4) + coefs[26]*(isq4)*(jsq2) + coefs[27]*isq4*jsq3 + coefs[28]*(isq4)*(jsq4) + coefs[29]*(isq5) + coefs[30]*(isq5)*(jsq2) + coefs[31]*isq5*jsq3+ coefs[32]*(isq6) + coefs[33]*(isq6)*(jsq2) + coefs[34]*(isq7) + coefs[35]*(isq8))<1;
  }

As before, we wrap this in extern “C”{} for libraries.

Setup Multi-GPU Julia Driver

Recall that we are starting with the following parameters:

  imin = -12
  imax = 1
  jmin = -4
  jmax = 4
  iarr = convert(Vector{Float32},collect(imin:dx:imax))
  jarr = convert(Vector{Float32},collect(jmin:dx:jmax))
  sizei = length(imin:dx:imax)
  sizej = length(jmin:dx:jmax)
  totArea = ((imax-imin)*(jmax-jmin)/(sizei*sizej));
 
  coefs = getCoefficients(A0,A1,B0,B1,α,β1,β2,β3,β4)

Where getCoefficients is some function which returns an array of 36 integers. You can make this be a call for random integers or something of the like. Now we need to call our kernal from Julia. Start by compling the kernal as in part two into a .ptx. Our simple implementation will be to split the job by the number of cores on each GPU. On Comet, each part of the K80 has 2496 CUDA cores, so we would set

  cudaCores = [2496,2496]

I will instead use the more interesting case of my development computer. It has a GTX 970 with 1664 cores and a GTX 750Ti with 640 cores. Therefore I start by setting

  cudaCores = [1664,640]

The implementation is then as follows: I first get equalDiv as the number of calculations to be done per core. Since I am looping over a mesh with sizei and sizej, if I let totCores=sum(cudaCores) be the total number of cores, then

equalDiv = sizei*sizej÷totCores + 1

tells me how many calculations per core (we add 1 (or take the ceiling) in order to make sure that we cover all of it. Otherwise the part truncated from the integer division will not be calculated). Next we need to calculate where to start the second GPU. Let portions=equalDiv*cudaCores be the total number of calculations in each GPU (it returns a vector of 2 values). I want my code to work when there’s only 1 card (i.e. cudaCores=[2946]), so to calculate the starting indices I run

  if numCards > 1
    startIdx = [0 cumsum(portions)[1:end-1]]
  else
    startIdx = [0]
  end

What this does is give an array where the first value is zero, the second value is portions[1], the third is portions[1]+portions[2], etc., and if there is only one card then it’s simply the array with zero. Notice this is exactly the index which the CUDA kernal needs to stop at, so this works.

Now we need to move our arrays over to the GPU. Note that each array is stored on only one GPU, and so we need to loop through the devices and put each array on each device. We change devices with with command device(i), where i=0 is the first device, i=1 is the second, etc. Since the values are actually C-pointers, we will just store them in arrays of type Any (of size numCards which is the number of GPU cards as calculated by the length(cudaCores)). The setup is then:

  g_iarr = Vector{Any}(numCards)
  g_jarr = Vector{Any}(numCards)
  g_tmp = Vector{Any}(numCards)
  g_coefs = Vector{Any}(numCards)
  ans = Vector{Int32}(numCards)
  integrationFuncs = Vector{Any}(numCards)
  CUDArt.init(devices(dev->true))
  devlist = devices(dev->true)
  streams = [(device(dev); Stream()) for dev in devlist]
  for i = 1:numCards
    device(i-1)
    g_iarr[i]  = CudaArray(iarr)
    g_jarr[i]  = CudaArray(jarr)
    g_tmp[i]   = CudaArray(Int32,cudaCores[i])
    md = CuModule("integration.ptx",false)
    integrationFuncs[i] = CuFunction(md,"integration")
  end

Lastly, we need to call the kernal. Recall that in my problem the inner loop is to change coefs, run the kernal calculation, and use the result. Thus in my test function is where I send coefs to the GPU. This will call the kernal as before, except we need to do this asynchronously via Julia’s streams. Notice we have a new variable (or array of variables) around: streams. The code initiated 2 GPU streams, one on each device. Thus what we will do is tell the kernal to run on the stream, and move onto the calculation before it finishes (but tell it to not sum the result until after the GPU stream finished). This is done by the following code:

        @async begin
          dev = device(i-1)
          g_coefs[i] = CudaArray(coefs)
          launch(integrationFuncs[i], cudaCores[i], 64, (g_coefs[i], g_iarr[i], g_jarr[i], sizei,sizej,equalDiv,startIdx[i],g_tmp[i],),stream=streams[i]);
          wait(streams[i])
          ans[i] = sum(to_host(g_tmp[i]))
        end

@async is the command which asynchronizes, as in Julia keeps going forward even if the command isn’t done. Thus what we need to do is run all of the GPUs and then wait for each to finish via the @sync command. The full loop is then as follows:

  function f4()
    @sync begin
      for i = 1:numCards
        @async begin
          dev = device(i-1)
          g_coefs[i] = CudaArray(coefs)
          launch(integrationFuncs[i], cudaCores[i], 64, (g_coefs[i], g_iarr[i], g_jarr[i], sizei,sizej,equalDiv,startIdx[i],g_tmp[i],),stream=streams[i]);
          wait(streams[i])
          ans[i] = sum(to_host(g_tmp[i]))
        end
      end
    end
    res = sum(ans)*totArea
    #println(res)
  end

I put it in the function f4 for benchmarking. Notice we have @sync around the inner loop, telling it not to go past the loop until each portion is done, but in the loop we wrap it with @async so that way Julia can start the GPU codes all at the same time without having to wait for the first to finish, and then as they finish it comes back to finish up (this is not needed to be done in parallel since the overhead for doing this is really small. The overhead of @parallel would probably increase the runtime!). After we are done, we scale the area to get the answer.

So how well did it do? On my last post someone told me to checkout the benchmark package. So to finish off the code I run:

  df4 = benchmark(f4,"MultiGPU",1000)
  println(df4)
  CUDArt.close(devices(dev->true))

benchmark will run the function 1000 times and tell me the average runtime by printing the dataframe df4. Then I close the GPU to clean up the memory.

Heterogeneous GPU Setup

Recall that our last implementation simply split up the problem by how many cores each GPU has. We will get back to whether that is correct or not later, but first lets make something a little more complicated to test this out. So what about making equalDiv higher on faster GPUs and slower on slower GPUs? What we will do is declare an array trueBias, like

trueBias = [.75,.25]

which will say how to bias the equalDivs amongst the GPUs. How do we calculate the division? It’s easiest to do this by example. Notice in the code above we have that

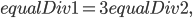
equalDiv1 = 3 equalDiv2,

that is equalDiv is 3 times the size on the first GPU than the second GPU. Since the number of values we want to calculate is sizei*sizej, and we calculate equalDiv values on cudaCores[i] different cores, the total amount that we calculate is

equalDiv1*cudaCores1 + equalDiv2*cudaCores2 = sizei*sizej

and by substitution we then get

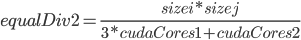
equalDiv2 = frac{sizei*sizej}{3*cudaCores1+cudaCores2}

Do a bigger example with [.75, 1/16, 1/8, 1/16]. See the pattern? Notice that trueBias/trueBias[i] gives us the value that we need to substitute $k$ with $i$ (where $k$ is the value on the top). Then notice that the left hand side is simply the dot product of these values with the number of cudaCores. Thus we pull out equalDivi and sizei*sizej by that dot product to get what equalDivi should be the final result is that the following calculates the desired quantity:

  equalDiv = Vector{Int32}(numCards)
  for i = 1:numCards
    equalDiv[i] = ceil(Int32,(sizei*sizej)/dot(trueBias/(trueBias[i]),cudaCores))
  end

We then need to make sure we scale portions by the equalDiv per GPU:

  portions = equalDiv.*cudaCores
  if numCards > 1
    startIdx = [0 cumsum(portions)[1:end-1]]
  else
    startIdx = [0]
  end

When calling the kernal, all we have to do is specify which equalDiv we want to use, and thus we get the test function:

  function f5()
    @sync begin
      for i = 1:numCards
        @async begin
          dev = device(i-1)
          g_coefs[i] = CudaArray(coefs)
          launch(integrationFuncs[i], cudaCores[i], 64, (g_coefs[i], g_iarr[i], g_jarr[i], sizei,sizej,equalDiv[i],startIdx[i],g_tmp[i],),stream=streams[i]);
          wait(streams[i])
          ans[i] = sum(to_host(g_tmp[i]))
        end
      end
    end
    res = sum(ans)*totArea
    #println(res)
  end
  df5 = benchmark(f5,"MultiGPU2",1000)
  println(df5)
  CUDArt.close(devices(dev->true))

Same as before with equalDiv[i] now.

Does Changing the Divisions Help?

I ran this on my desktop and got the following results:

1x12 DataFrames.DataFrame
| Row | Category | Benchmark | Iterations | TotalWall | AverageWall |
|-----|----------|-----------|------------|-----------|-------------|
| 1   | "GPU"    | "GPU"     | 1000       | 23.1013   | 0.0231013   |
 
| Row | MaxWall   | MinWall  | Timestamp             |
|-----|-----------|----------|-----------------------|
| 1   | 0.0264843 | 0.021724 | "2016-02-27 17:16:32" |
 
| Row | JuliaHash                                  | CodeHash | OS        |
|-----|--------------------------------------------|----------|-----------|
| 1   | "a2f713dea5ac6320d8dcf2835ac4a37ea751af05" | NA       | "Windows" |
 
| Row | CPUCores |
|-----|----------|
| 1   | 8        |
1x12 DataFrames.DataFrame
| Row | Category   | Benchmark  | Iterations | TotalWall | AverageWall |
|-----|------------|------------|------------|-----------|-------------|
| 1   | "MultiGPU" | "MultiGPU" | 1000       | 22.3445   | 0.0223445   |
 
| Row | MaxWall   | MinWall   | Timestamp             |
|-----|-----------|-----------|-----------------------|
| 1   | 0.0593403 | 0.0211532 | "2016-02-27 17:16:55" |
 
| Row | JuliaHash                                  | CodeHash | OS        |
|-----|--------------------------------------------|----------|-----------|
| 1   | "a2f713dea5ac6320d8dcf2835ac4a37ea751af05" | NA       | "Windows" |
 
| Row | CPUCores |
|-----|----------|
| 1   | 8        |
1x12 DataFrames.DataFrame
| Row | Category    | Benchmark   | Iterations | TotalWall | AverageWall |
|-----|-------------|-------------|------------|-----------|-------------|
| 1   | "MultiGPU2" | "MultiGPU2" | 1000       | 22.5787   | 0.0225787   |
 
| Row | MaxWall   | MinWall   | Timestamp             |
|-----|-----------|-----------|-----------------------|
| 1   | 0.0557531 | 0.0213999 | "2016-02-27 17:17:18" |
 
| Row | JuliaHash                                  | CodeHash | OS        |
|-----|--------------------------------------------|----------|-----------|
| 1   | "a2f713dea5ac6320d8dcf2835ac4a37ea751af05" | NA       | "Windows" |
 
| Row | CPUCores |
|-----|----------|
| 1   | 8        |
1x12 DataFrames.DataFrame
| Row | Category             | Benchmark            | Iterations | TotalWall |
|-----|----------------------|----------------------|------------|-----------|
| 1   | "MultiGPU2-Balanced" | "MultiGPU2-Balanced" | 1000       | 22.3453   |
 
| Row | AverageWall | MaxWall   | MinWall   | Timestamp             |
|-----|-------------|-----------|-----------|-----------------------|
| 1   | 0.0223453   | 0.0593927 | 0.0211599 | "2016-02-27 17:17:41" |
 
| Row | JuliaHash                                  | CodeHash | OS        |
|-----|--------------------------------------------|----------|-----------|
| 1   | "a2f713dea5ac6320d8dcf2835ac4a37ea751af05" | NA       | "Windows" |
 
| Row | CPUCores |
|-----|----------|
| 1   | 8        |

The first run was 1 GPU which averaged .0231 seconds. The second run was equal splitting which got .0223 seconds. Next was the split trueBias = [.51,.49] which got .0225 seconds. Lastly I set trueBias = [.5,.5] and got .0223 seconds. Thus notice two things: one allowing for the homogeneous split has no overhead (we still only pass an integer), but more interesting, the best split was still 50-50. This is reproducible and only gets worse when we split more ([.75,.25] is terrible!).

So what’s going on? Well, first of all notice that this is not a memory bound problem: in the loop we only send an array of 36 values. The largest difference between the GPUs is their memory bandwidth. From the GTX 970 specs we see that its memory bandwidth is 224 GB/sec, vs the GTX 750Ti’s 86.4 GB/sec. That’s a whopping 2.5x difference, but it doesn’t matter in this case. All that matters in this test is the compute power. Here the GTX 970 has a base clock of 1050 MHz and a boost clock of 1178 MHz, while the GTX 750Ti has a base clock of 1020 MHz and a boost clock of 1085 MHz. 1178/1085 = 1.08. They are almost the same. Note that this is the difference between a entry level graphics card from ~4 years ago, vs one of the high-end cards of today (only beat in the gaming sphere by the GTX 980(Ti) and the Titan X). GPUs tend to have about the same strength per core, while the difference is mostly in how many cores there are. In that sense, our result is not surprising. However, knowing how to deal with the heterogeneity is probably good for more memory taxing problems.

Running it on Comet

I compiled this code onto Comet and ran it with the job script

#!/bin/bash
#SBATCH -A uci128
#SBATCH --job-name="jOpt"
#SBATCH --output="output/jOpt.%j.%N.out"
#SBATCH --partition=gpu-shared
#SBATCH --gres=gpu:2
#SBATCH --nodes=1
#SBATCH --export=ALL
#SBATCH --mail-type=ALL
#SBATCH --mail-user=crackauc@uci.edu
#SBATCH --ntasks-per-node=12
#SBATCH -t 0:10:00
module load cuda/7.0
module load cmake
export SLURM_NODEFILE=`generate_pbs_nodefile`
/home/crackauc/julia-a2f713dea5/bin/julia --machinefile $SLURM_NODEFILE /home/crackauc/projectCode/ImprovedSRK/Optimization/integrationTestComet.jl

The result was the following:

| Row | Category    | Benchmark   | Iterations | TotalWall | AverageWall |
|-----|-------------|-------------|------------|-----------|-------------|
| 1   | "SingleGPU" | "SingleGPU" | 1000       | 26.5858   | 0.0265858   |
 
| Row | MaxWall   | MinWall   | Timestamp             |
|-----|-----------|-----------|-----------------------|
| 1   | 0.0440866 | 0.0260225 | "2016-02-27 17:28:41" |
 
| Row | JuliaHash                                  | CodeHash | OS      |
|-----|--------------------------------------------|----------|---------|
| 1   | "a2f713dea5ac6320d8dcf2835ac4a37ea751af05" | NA       | "Linux" |
 
| Row | CPUCores |
|-----|----------|
| 1   | 24       |
 
1x12 DataFrames.DataFrame
| Row | Category   | Benchmark  | Iterations | TotalWall | AverageWall |
|-----|------------|------------|------------|-----------|-------------|
| 1   | "MultiGPU" | "MultiGPU" | 1000       | 22.3377   | 0.0223377   |
 
| Row | MaxWall   | MinWall   | Timestamp             |
|-----|-----------|-----------|-----------------------|
| 1   | 0.0458176 | 0.0219705 | "2016-02-27 17:29:06" |
 
| Row | JuliaHash                                  | CodeHash | OS      |
|-----|--------------------------------------------|----------|---------|
| 1   | "a2f713dea5ac6320d8dcf2835ac4a37ea751af05" | NA       | "Linux" |
 
| Row | CPUCores |
|-----|----------|
| 1   | 24       |
1x12 DataFrames.DataFrame
| Row | Category             | Benchmark            | Iterations | TotalWall |
|-----|----------------------|----------------------|------------|-----------|
| 1   | "MultiGPU2-Balanced" | "MultiGPU2-Balanced" | 1000       | 22.4148   |
 
| Row | AverageWall | MaxWall   | MinWall   | Timestamp             |
|-----|-------------|-----------|-----------|-----------------------|
| 1   | 0.0224148   | 0.0549695 | 0.0220449 | "2016-02-27 17:29:29" |
 
| Row | JuliaHash                                  | CodeHash | OS      |
|-----|--------------------------------------------|----------|---------|
| 1   | "a2f713dea5ac6320d8dcf2835ac4a37ea751af05" | NA       | "Linux" |
 
| Row | CPUCores |
|-----|----------|
| 1   | 24       |
1x12 DataFrames.DataFrame
| Row | Category               | Benchmark              | Iterations |
|-----|------------------------|------------------------|------------|
| 1   | "MultiGPU2-Unbalanced" | "MultiGPU2-Unbalanced" | 1000       |
 
| Row | TotalWall | AverageWall | MaxWall   | MinWall   |
|-----|-----------|-------------|-----------|-----------|
| 1   | 22.6683   | 0.0226683   | 0.0568948 | 0.0224583 |
 
| Row | Timestamp             | JuliaHash                                  |
|-----|-----------------------|--------------------------------------------|
| 1   | "2016-02-27 17:29:53" | "a2f713dea5ac6320d8dcf2835ac4a37ea751af05" |
 
| Row | CodeHash | OS      | CPUCores |
|-----|----------|---------|----------|
| 1   | NA       | "Linux" | 24       |

Notice that there is a performance gain by going to multiple GPUs, but again we loose performance by unbalancing (again, by running this a few times we see that the two version which are balanced are the same result within random error). Still, the speedup from going to multiple GPUs is not large here. The difference is bigger for bigger meshes. This shows you that multiple GPUs is really good for tackling larger problems, though in general if your problem is “not too big”, then going to multiple GPUs will only be a mild gain (remember, you want each processor to run enough calculations for it to be worthwhile!).

Lastly, notice that there is not much of a performance difference from our consumer GPU and the Tesla! This is for two reasons. One, we are using single precision. The Tesla and GTX line are almost the the same when it comes to single precision calculations. We would see a huge (~32x) difference for double precision calculations. Secondly, the Tesla has ECC memory which slows it down a little but makes sure it does not have errors in its memory. Lastly, the big advantage of a Tesla K80 is that it has a “huge” amount of memory compared to other GPUs. The GTX 970 has ~3.6 GB (due to NVIDIA’s lies…) whereas the Tesla K80 has 24 GB. This means that if the problem is single precision and fits on your GTX you’re fine. Otherwise, the Tesla is required.

Where do we go from here?

We started with an HPC allocation. We got Julia running on the HPC, and we setup a parallel function to use multiple nodes. Then, realizing how parallel our problem is, we took it to GPUs, first taking on one GPU, and then multiple, with a setup that works for as many GPUs as you need. Our implementation is about a kernal which simply evaluates a function along a vector, i.e. a vectorized function call. Thus very similar code to this works for all vectorized functions. What else do we need?

One obvious generalization is higher dimension arrays. If you need to do vectorized calls on matrices etc., you can just vectorize them in Julia and send them to the GPU in that form. If you want to be able to keep the matrix form in the CUDA kernal, you just have to play with indices but the same approach we did here works.

One place to go is to now start using Float64’s (doubles). Remember, on most GPUs they are really slow, but on the Tesla GPUs like in Comet they are still quite fast. All you have to do is change the array declarations to Float64’s and now you have double precision.

This means that you can basically code whatever vectorized calls you need to do. What about harder problems? If you need harder problems, check out libraries. cuBLAS is a BLAS implementation for doing linear algebra on the GPU. It contains cuBLASxt which automatically scales cuBLAS to multiple GPUs. Another thing for linear algebra is cuSolver for GPU methods for solving the linear equation Ax=b. You can use these in your CUDA kernals.

There are also Julia packages for making this easier. There’s cuBLAS.jl, ArrayFire.jl, etc. all for making GPU calculations easier. These do not require you to write/compile CUDA kernals. I may write a tutorial on this with some experiments, but this should be pretty easy given what you know now.

At this point you should be pretty capable with GPUs. My next focus will then be on Xeon Phis. I will have to write a Multigrid solver soon, so I may write one on the GPU and also on the Xeon Phi (called from Julia) and see the performance difference. Since I also have an allocation on LSU’s SuperMIC, I will also be looking for good ways to both use the Xeon Phi at the same time as the GPU (they have hybrid nodes!) and understand which problems are better on which device. Stay tuned.

Full Julia Code

Again, I am going to put my full Julia code here for reference. I use a bunch of values to calculate the coefficients as it pertains to my real problem, but again you can just swap out the getCoefficients problem with any function that returns an array of 36 Float32’s (rand(36)).

function integrationTest()
  A0 = [0 0 0 0
      1 0 0 0
      1/4 1/4 0 0
      0 0 0 0];
  A1 = [0 0 0 0
      1/4 0 0 0
      1 0 0 0
      0 0 1/4 0];
  B0 = [0 0 0 0
       0 0 0 0
      1 1/2 0 0
      0 0 0 0];
  B1 = [0 0 0 0
      -1/2 0 0 0
      1 0 0 0
      2 -1 1/2 0];
 
  α = [1/6 1/6 2/3 0];
 
  β1 = [-1 4/3 2/3 0];
  β2 = [1 -4/3 1/3 0];
  β3 = [2 -4/3 -2/3 0];
  β4 = [-2 5/3 -2/3 1];
 
  dx = 1/400
 
 
 
  imin = -12
  imax = 1
  jmin = -4
  jmax = 4
  coefs,powz,poww = getCoefficients(A0,A1,B0,B1,α,β1,β2,β3,β4)
  iarr = convert(Vector{Float32},collect(imin:dx:imax))
  jarr = convert(Vector{Float32},collect(jmin:dx:jmax))
  sizei = length(imin:dx:imax)
  sizej = length(jmin:dx:jmax)
  totArea = ((imax-imin)*(jmax-jmin)/(sizei*sizej));
 
  #=
  function coefFunc()
    getCoefficients(A0,A1,B0,B1,α,β1,β2,β3,β4)
  end
  dfcoef = benchmark(coefFunc,"coef",10)
  println(dfcoef)
  =#
 
  #=
  #Some SIMD
  function f1()
    res = @sync @parallel (+) for i = imin:dx:imax
      tmp = 0
       for j=jmin:dx:jmax
        ans = 0
        @simd for k=1:36
          @inbounds ans += coefs[k]*(i^(powz[k]))*(j^(poww[k]))
        end
        tmp += abs(ans)<1
      end
      tmp
    end
    res = res*((imax-imin)*(jmax-jmin)/(length(imin:dx:imax)*length(jmin:dx:jmax)))
    println(res)#Mathematica gives 2.98
  end
  df1 = benchmark(f1,"CPUSimp",2)
  println(df1)
  =#
  #=
  ## Full unravel
  function f2()
    res = @sync @parallel (+) for i = imin:dx:imax
        tmp = 0
        isq2 = i*i; isq3 = i*isq2; isq4 = isq2*isq2; isq5 = i*isq4
        isq6 = isq4*isq2; isq7 = i*isq6; isq8 = isq4*isq4
        @simd for j=jmin:dx:jmax
          jsq2 = j*j; jsq3= j*jsq2; jsq4 = jsq2*jsq2;
          jsq5 = j*jsq4; jsq6 = jsq2*jsq4; jsq7 = j*jsq6; jsq8 = jsq4*jsq4
          @inbounds tmp += abs(coefs[1]*(jsq2) + coefs[2]*(jsq3) + coefs[3]*(jsq4) + coefs[4]*(jsq5) + coefs[5]*jsq6 + coefs[6]*jsq7 + coefs[7]*jsq8 + coefs[8]*(i) + coefs[9]*(i)*(jsq2) + coefs[10]*i*jsq3
          + coefs[11]*(i)*(jsq4) + coefs[12]*i*jsq5 + coefs[13]*(i)*(jsq6) + coefs[14]*i*jsq7 + coefs[15]*(isq2) + coefs[16]*(isq2)*(jsq2) + coefs[17]*isq2*jsq3 + coefs[18]*(isq2)*(jsq4) +
          coefs[19]*isq2*jsq5 + coefs[20]*(isq2)*(jsq6) + coefs[21]*(isq3) + coefs[22]*(isq3)*(jsq2) + coefs[23]*isq3*jsq3 + coefs[24]*(isq3)*(jsq4) + coefs[25]*isq3*jsq5 +
          coefs[26]*(isq4) + coefs[27]*(isq4)*(jsq2) + coefs[28]*isq4*jsq3 + coefs[29]*(isq4)*(jsq4) + coefs[30]*(isq5) + coefs[31]*(isq5)*(jsq2) + coefs[32]*isq5*jsq3+ coefs[33]*(isq6) +
          coefs[34]*(isq6)*(jsq2) + coefs[35]*(isq7) + coefs[36]*(isq8))<1
        end
        tmp
      end
      res = res*totArea
      println(res)#Mathematica gives 2.98
  end
  df2 = benchmark(f2,"CPU",2)
  println(df2)
  =#
 
  #=
  #GPU
  cudaCores = 2496;
  equalDiv = sizei*sizej÷cudaCores + 1
  CUDArt.init(devices(dev->true))
  dev = device(0)
  md = CuModule("integrationWin.ptx",false)
  integrationFunc = CuFunction(md,"integration")
  g_iarr = CudaArray(iarr)
  g_jarr = CudaArray(jarr)
  g_tmp = CudaArray(Int32,cudaCores)
  function f3()
    g_coefs = CudaArray(coefs)
    launch(integrationFunc, cudaCores, 64, (g_coefs, g_iarr, g_jarr, sizei,sizej,equalDiv,g_tmp,)); res = sum(to_host(g_tmp));
    res = res*totArea
    #println(res)
  end
  df3 = benchmark(f3,"GPU",10)
  println(df3)
  CUDArt.close(devices(dev->true))
  =#
 
  #Single-GPU
  cudaCores = [2496];
  #cudaCores = [1664,1]
  numCards = length(cudaCores)
  totCores = sum(cudaCores)
  equalDiv = sizei*sizej÷totCores + 1
  portions = equalDiv*cudaCores
  if numCards > 1
    startIdx = [0 cumsum(portions)[1:end-1]]
  else
    startIdx = [0]
  end
  g_iarr = Vector{Any}(numCards)
  g_jarr = Vector{Any}(numCards)
  g_tmp = Vector{Any}(numCards)
  g_coefs = Vector{Any}(numCards)
  ans = Vector{Int32}(numCards)
  integrationFuncs = Vector{Any}(numCards)
  CUDArt.init(devices(dev->true))
  devlist = devices(dev->true)
  streams = [(device(dev); Stream()) for dev in devlist]
  for i = 1:numCards
    device(i-1)
    g_iarr[i]  = CudaArray(iarr)
    g_jarr[i]  = CudaArray(jarr)
    g_tmp[i]   = CudaArray(Int32,cudaCores[i])
    md = CuModule("integration.ptx",false)
    integrationFuncs[i] = CuFunction(md,"integration")
  end
 
  function f4()
    @sync begin
      for i = 1:numCards
        @async begin
          dev = device(i-1)
          g_coefs[i] = CudaArray(coefs)
          launch(integrationFuncs[i], cudaCores[i], 64, (g_coefs[i], g_iarr[i], g_jarr[i], sizei,sizej,equalDiv,startIdx[i],g_tmp[i],),stream=streams[i]);
          wait(streams[i])
          ans[i] = sum(to_host(g_tmp[i]))
        end
      end
    end
    res = sum(ans)*totArea
    println(res)
  end
  df4 = benchmark(f4,"SingleGPU",1000)
  println(df4)
  CUDArt.close(devices(dev->true))
 
  #Multi-GPU
  cudaCores = [2496,2496];
  #cudaCores = [1664,1]
  numCards = length(cudaCores)
  totCores = sum(cudaCores)
  equalDiv = sizei*sizej÷totCores + 1
  portions = equalDiv*cudaCores
  if numCards > 1
    startIdx = [0 cumsum(portions)[1:end-1]]
  else
    startIdx = [0]
  end
  g_iarr = Vector{Any}(numCards)
  g_jarr = Vector{Any}(numCards)
  g_tmp = Vector{Any}(numCards)
  g_coefs = Vector{Any}(numCards)
  ans = Vector{Int32}(numCards)
  integrationFuncs = Vector{Any}(numCards)
  CUDArt.init(devices(dev->true))
  devlist = devices(dev->true)
  streams = [(device(dev); Stream()) for dev in devlist]
  for i = 1:numCards
    device(i-1)
    g_iarr[i]  = CudaArray(iarr)
    g_jarr[i]  = CudaArray(jarr)
    g_tmp[i]   = CudaArray(Int32,cudaCores[i])
    md = CuModule("integration.ptx",false)
    integrationFuncs[i] = CuFunction(md,"integration")
  end
 
  function f4()
    @sync begin
      for i = 1:numCards
        @async begin
          dev = device(i-1)
          g_coefs[i] = CudaArray(coefs)
          launch(integrationFuncs[i], cudaCores[i], 64, (g_coefs[i], g_iarr[i], g_jarr[i], sizei,sizej,equalDiv,startIdx[i],g_tmp[i],),stream=streams[i]);
          wait(streams[i])
          ans[i] = sum(to_host(g_tmp[i]))
        end
      end
    end
    res = sum(ans)*totArea
    println(res)
  end
  df4 = benchmark(f4,"MultiGPU",1000)
  println(df4)
  CUDArt.close(devices(dev->true))
 
 
  #= Hardware Bias Spec.
  cudaCores = [1664,640];
  trueBias = [.75,.25]
  numCards = length(cudaCores)
  totCores = sum(cudaCores)
  coreBias = cudaCores ./ totCores
  workloadBias = trueBias./(coreBias)
  equalDiv = ceil(Int32,sizei*sizej/totCores .* workloadBias)
  portions = equalDiv.*cudaCores
  if numCards > 1
    startIdx = [0 cumsum(portions)[1:end-1]]
  else
    startIdx = [0]
  end
  =#
 
  ##Heterogenous Multi-GPU
  # trueBias = coreBias.* workloadBias*numCards
  cudaCores = [2496,2496]
  trueBias = [.5,.5]
  numCards = length(cudaCores)
  totCores = sum(cudaCores)
  equalDiv = Vector{Int32}(numCards)
  for i = 1:numCards
    equalDiv[i] = ceil(Int32,(sizei*sizej)/dot(trueBias/(trueBias[i]),cudaCores))
  end
 
  portions = equalDiv.*cudaCores
  if numCards > 1
    startIdx = [0 cumsum(portions)[1:end-1]]
  else
    startIdx = [0]
  end
  g_iarr = Vector{Any}(numCards)
  g_jarr = Vector{Any}(numCards)
  g_tmp = Vector{Any}(numCards)
  g_coefs = Vector{Any}(numCards)
  ans = Vector{Int32}(numCards)
  integrationFuncs = Vector{Any}(numCards)
  CUDArt.init(devices(dev->true))
  devlist = devices(dev->true)
  streams = [(device(dev); Stream()) for dev in devlist]
  for i = 1:numCards
    device(i-1)
    g_iarr[i]  = CudaArray(iarr)
    g_jarr[i]  = CudaArray(jarr)
    g_tmp[i]   = CudaArray(Int32,cudaCores[i])
    md = CuModule("integration.ptx",false)
    integrationFuncs[i] = CuFunction(md,"integration")
  end
 
  function f5()
    @sync begin
      for i = 1:numCards
        @async begin
          dev = device(i-1)
          g_coefs[i] = CudaArray(coefs)
          launch(integrationFuncs[i], cudaCores[i], 64, (g_coefs[i], g_iarr[i], g_jarr[i], sizei,sizej,equalDiv[i],startIdx[i],g_tmp[i],),stream=streams[i]);
          wait(streams[i])
          ans[i] = sum(to_host(g_tmp[i]))
        end
      end
    end
    res = sum(ans)*totArea
    #println(res)
  end
  df5 = benchmark(f5,"MultiGPU2-Balanced",1000)
  println(df5)
  CUDArt.close(devices(dev->true))
 
 
 
  ##Heterogenous Multi-GPU
  # trueBias = coreBias.* workloadBias*numCards
  cudaCores = [2496,2496];
  trueBias = [.55,.45]
  numCards = length(cudaCores)
  totCores = sum(cudaCores)
  equalDiv = Vector{Int32}(numCards)
  for i = 1:numCards
    equalDiv[i] = ceil(Int32,(sizei*sizej)/dot(trueBias/(trueBias[i]),cudaCores))
  end
 
  portions = equalDiv.*cudaCores
  if numCards > 1
    startIdx = [0 cumsum(portions)[1:end-1]]
  else
    startIdx = [0]
  end
  g_iarr = Vector{Any}(numCards)
  g_jarr = Vector{Any}(numCards)
  g_tmp = Vector{Any}(numCards)
  g_coefs = Vector{Any}(numCards)
  ans = Vector{Int32}(numCards)
  integrationFuncs = Vector{Any}(numCards)
  CUDArt.init(devices(dev->true))
  devlist = devices(dev->true)
  streams = [(device(dev); Stream()) for dev in devlist]
  for i = 1:numCards
    device(i-1)
    g_iarr[i]  = CudaArray(iarr)
    g_jarr[i]  = CudaArray(jarr)
    g_tmp[i]   = CudaArray(Int32,cudaCores[i])
    md = CuModule("integration.ptx",false)
    integrationFuncs[i] = CuFunction(md,"integration")
  end
 
  function f5()
    @sync begin
      for i = 1:numCards
        @async begin
          dev = device(i-1)
          g_coefs[i] = CudaArray(coefs)
          launch(integrationFuncs[i], cudaCores[i], 64, (g_coefs[i], g_iarr[i], g_jarr[i], sizei,sizej,equalDiv[i],startIdx[i],g_tmp[i],),stream=streams[i]);
          wait(streams[i])
          ans[i] = sum(to_host(g_tmp[i]))
        end
      end
    end
    res = sum(ans)*totArea
    #println(res)
  end
  df5 = benchmark(f5,"MultiGPU2-Unbalanced",1000)
  println(df5)
  CUDArt.close(devices(dev->true))
end
 
using CUDArt
using Benchmark
include("getCoefs.jl")
integrationTest()

The post Multiple-GPU Parallelism on the HPC with Julia appeared first on Stochastic Lifestyle.

Tutorial for Julia on the HPC with GPUs

By: Christopher Rackauckas

Re-posted from: http://www.stochasticlifestyle.com/julia-on-the-hpc-with-gpus/

This is a continuous of my previous post on using Julia on the XSEDE Comet HPC. Check that out first for an explanation of the problem. In that problem, we wished to solve for the area of a region where a polynomial was less than 1, which was calculated by code like:

@time res = @sync @parallel (+) for i = imin:dx:imax
  tmp = 0
  isq2 = i*i; isq3 = i*isq2; isq4 = isq2*isq2; isq5 = i*isq4
  isq6 = isq4*isq2; isq7 = i*isq6; isq8 = isq4*isq4
  @simd for j=jmin:dx:jmax
    jsq2 = j*j; jsq3= j*jsq2; jsq4 = jsq2*jsq2;
    jsq5 = j*jsq4; jsq6 = jsq2*jsq4; jsq7 = j*jsq6; jsq8 = jsq4*jsq4
    @inbounds tmp += abs(coefs[1]*(jsq2) + coefs[2]*(jsq3) + coefs[3]*(jsq4) + coefs[4]*(jsq5) + coefs[5]*jsq6 + coefs[6]*jsq7 + coefs[7]*jsq8 + coefs[8]*(i) + coefs[9]*(i)*(jsq2) + coefs[10]*i*jsq3
    + coefs[11]*(i)*(jsq4) + coefs[12]*i*jsq5 + coefs[13]*(i)*(jsq6) + coefs[14]*i*jsq7 + coefs[15]*(isq2) + coefs[16]*(isq2)*(jsq2) + coefs[17]*isq2*jsq3 + coefs[18]*(isq2)*(jsq4) +
    coefs[19]*isq2*jsq5 + coefs[20]*(isq2)*(jsq6) + coefs[21]*(isq3) + coefs[22]*(isq3)*(jsq2) + coefs[23]*isq3*jsq3 + coefs[24]*(isq3)*(jsq4) + coefs[25]*isq3*jsq5 +
    coefs[26]*(isq4) + coefs[27]*(isq4)*(jsq2) + coefs[28]*isq4*jsq3 + coefs[29]*(isq4)*(jsq4) + coefs[30]*(isq5) + coefs[31]*(isq5)*(jsq2) + coefs[32]*isq5*jsq3+ coefs[33]*(isq6) +
    coefs[34]*(isq6)*(jsq2) + coefs[35]*(isq7) + coefs[36]*(isq8))<1
  end
  tmp
end
res = res*((imax-imin)*(jmax-jmin)/(length(imin:dx:imax)*length(jmin:dx:jmax)))
println(res)

Notice that this code is massively parallel: at every point we do something and we just sum the values. This means it’s a perfect problem for the GPU. I am going to show you how to do this.

Getting CUDArt Setup

We will be using the CUDArt.jl package. I first had this working with the CUDA.jl package but was informed that going forward we should be using the CUDArt.jl package. There’s really not much of a difference in my implementation.

To get started, you have to go here and install an appropriate version of CUDA. Note that you have to have an NVIDIA GPU in order to do this. I will be using a GTX970 on one computer (Windows), and a GTX980Ti on another. Comet has a queue with 2x Tesla K80s, but that’s probably overkill and you should try to develop locally first. One you have all of that setup, CUDArt.jl should compile some .ptx files upon first use. If it does, you’re good to go.

CUDArt.jl’s page shows you how to get started. However, I am going to add a little caveat. In reality, this is the objective function in a machine learning problem, and so we wish to be able to recompute this as quickly as possible just by swapping out the coefficient array coefs. Therefore all of the other arrays must persist on the GPU.

Here’s what we’re going to do. To maximize performance on the GPU we will use Float32’s. On most GPUs (all except the Teslas and the Titan Black), the double precision floating point capabilities are SEVERELY gimped in comparison (1/32 the performance…). To do this, we setup our calculations as follows:

## Setup CPU-side parameters
imin = -8
imax = 1
jmin = -3
jmax = 3
@time coefs,powz,poww = getCoefficients(A0,A1,B0,B1,α,β1,β2,β3,β4)
iarr = convert(Vector{Float32},collect(imin:dx:imax))
jarr = convert(Vector{Float32},collect(jmin:dx:jmax))
sizei = length(imin:dx:imax)
sizej = length(jmin:dx:jmax)
cudaCores = 1664;
equalDiv = sizei*sizej÷cudaCores + 1
 
##GPU Code
CUDArt.init(devices(dev->true)) #Initiate the devices
dev = device(0) #Set the GPU to the first GPU
#Move the arrays over
g_iarr = CudaArray(iarr)
g_jarr = CudaArray(jarr)
g_coefs = CudaArray(coefs)
g_tmp = CudaArray(Int32,cudaCores)

Note that if you have multiple GPUs and don’t know which one is which device, you can use the command CUDArt.name(CUDArt.device_properties(number)). Here I have CUDArt.name(CUDArt.device_properties(0)) return “GeForce GTX 970” and CUDArt.name(CUDArt.device_properties(1)) returns “GeForce GTX 750 Ti”, so I use device(0) to use the 970. Note that at any time you can change the device with this command, but be careful since the CudaArrays are stored on the device that you call them from. If you want to use multiple GPUs, you will also need to split up your arrays.

The CUDA Kernal

Now the last thing I need to do is make my function. To do this, we have to go to C. Here is the Cuda kernal for the calculation:

// filename: integration.cu
// Performs the inner integration loop
extern "C"
{
    __global__ void integration(const float *coefs, const float *iArr, const float *jArr, const int sizei, const int sizej, const int equalDiv, int *tmp)
    {
        int index = threadIdx.x + blockIdx.x * blockDim.x;
        int loopInd;
        float i, j, isq2, isq3, isq4, isq5, isq6, isq7, isq8, jsq2, jsq3, jsq4, jsq5, jsq6, jsq7, jsq8,
        int ans = 0;
        for(loopInd=0;loopInd<equalDiv;loopInd=loopInd+1){
          i = iArr[(index*equalDiv+loopInd)/sizej];
          j = jArr[(index*equalDiv+loopInd)%sizej];
          if(index*equalDiv+loopInd >= sizei*sizej){
            break;
          }
          if((index*equalDiv+loopInd)%sizej==0 || loopInd==0){
            isq2 = i*i;
            isq3 = i*isq2;
            isq4 = isq2*isq2;
            isq5 = i*isq4;
            isq6 = isq4*isq2;
            isq7 = i*isq6;
            isq8 = isq4*isq4;
          }
          jsq2 = j*j;
          jsq3 = j*jsq2;
          jsq4 = jsq2*jsq2;
          jsq5 = j*jsq4;
          jsq6 = jsq2*jsq4;
          jsq7 = j*jsq6;
          jsq8 = jsq4*jsq4;
          /*tmp[index*1878+loopInd]= index*1878+loopInd;*/
		      /* changed to zero indexing */
          ans = ans + (abs(coefs[0]*(jsq2) + coefs[1]*(jsq3) + coefs[2]*(jsq4) + coefs[3]*(jsq5) + coefs[4]*jsq6 + coefs[5]*jsq7 + coefs[6]*jsq8 + coefs[7]*(i) + coefs[8]*(i)*(jsq2) + coefs[9]*i*jsq3 + coefs[10]*(i)*(jsq4) + coefs[11]*i*jsq5 + coefs[12]*(i)*(jsq6) + coefs[13]*i*jsq7 + coefs[14]*(isq2) + coefs[15]*(isq2)*(jsq2) + coefs[16]*isq2*jsq3 + coefs[17]*(isq2)*(jsq4) + coefs[18]*isq2*jsq5 + coefs[19]*(isq2)*(jsq6) + coefs[20]*(isq3) + coefs[21]*(isq3)*(jsq2) + coefs[22]*isq3*jsq3 + coefs[23]*(isq3)*(jsq4) + coefs[24]*isq3*jsq5 + coefs[25]*(isq4) + coefs[26]*(isq4)*(jsq2) + coefs[27]*isq4*jsq3 + coefs[28]*(isq4)*(jsq4) + coefs[29]*(isq5) + coefs[30]*(isq5)*(jsq2) + coefs[31]*isq5*jsq3+ coefs[32]*(isq6) + coefs[33]*(isq6)*(jsq2) + coefs[34]*(isq7) + coefs[35]*(isq8))<1);
        }
        tmp[index] = ans;
    }
}

Okay, that’s not nice looking at all, but it’s the same idea as the Julia script. Let me explain this code a little bit. Our function is integration. It takes in all of the variables and an array tmp which we will save the output to. The first call calculates a unique index for each CUDA core. We then setup our variables. Notice that before that we setup equalDiv to calculate how many calculations each core should do in order to evenly divide the work. Thus we loop over equalDiv times (and check if we go over since this will not necessarily come out perfectly). This means that each CUDA core will calculate the same number of (i,j)‘s. We then use the calculated index and the loop index to get our $i$ and $j$. We index down $j$ first, then go by $i$’s. This means it’s ordered as (0,0),(0,1),ldots,(0,J),(1,0),ldots. Notice that we achieve this by doing integer division by the size of the j array (truncation will make it an integer), and we get the $j$ index by moding by the size of the $j$ array. Using these $i$’s and $j$’s, we calculate the inner part of the loop. Notice that the calls to coefs had to be changed because C using 0-based indexing (as opposed to Julia’s 1-based indexing). Note that we can use the abs function from the CUDA math library. All of the CUDA math library functions are available.

[Note that when doing CUDA programming you want to allocate as little memory as possible. This is still on the small side so it worked out to be the optimal code. However, in some cases the non-unraveled version may be better due to the overhead of memory allocation.]

So there’s a template for you to play around with. When all of that is in order, we have to compile the kernal. On Windows with visual studio, I had to find out where cl.exe was (for me it was in Visual Studio 12’s directory) and tell the compiler the location of it. The total command was:

nvcc -ptx integration.cu -ccbin "C:Program Files (x86)Microsoft Visual Studio 12.0VCbin"

On Linux it was simpler:

nvcc -ptx integration.cu

From this you get .ptx files. To use the function in Julia, we then use the following code:

md = CuModule("integrationWin.ptx",false)
integrationFunc = CuFunction(md,"integration")
@time launch(integrationFunc, cudaCores, 64, (g_coefs, g_iarr, g_jarr, sizei,sizej,equalDiv,g_tmp,)); res = sum(to_host(g_tmp));
res = res*((imax-imin)*(jmax-jmin)/(length(imin:dx:imax)*length(jmin:dx:jmax)))
println(res)

What this does is take the “integration” function out of the .ptx and save it as integrationFunc. I can then call it at any time with the launch command. The second and third options are the grid and block sizes. In CUDA you always want to “overload”/overthread the cores so that there is no downtime. What I have found in my tests is that the best setting for this is to set the gridsize to the number of CUDA cores (since in our case these aren’t communicating) and overloading it by setting the block size to 64. Why 64? That worked out best in testing. Change the numbers around and see what works best for you.

The last argument to launch is the tuple of arguments for our integration function. Notice that there is a trailing comma, this is required. After the computation is finished, the results have been saved directly into g_tmp. Thus we send g_tmp to the host and sum up the results as before. We re-scale by the area of integration and that is the result.

Now in the actual objective function, what I want to do is update the coefficients to a new coefficients array, perform this calculation, and then move on. To do this I simply use the code:

    if gpuEnabled
      g_coefs = CudaArray(coefs)
      launch(integrationFunc, cudaCores, 64, (g_coefs, g_iarr, g_jarr, sizei,sizej,equalDiv,g_tmp,))
      res = sum(to_host(g_tmp))
      free(g_coefs)
    else ...

Notice I send coefs over to the GPU, run the kernal to get the answer, and then free up the GPU memory. So in my code I loop over this many times, changing coefs every time. When the entire computation is done, I finish with the command

CUDArt.close(devices(dev->true))

This will clear the GPU.

Comet?

These same steps will work on Comet. You will need to go into an interactive job to compile, but it should work fine. The job script to run Julia on the GPU node is:

#!/bin/bash
#SBATCH -A <account>
#SBATCH --job-name="jOpt"
#SBATCH --output="output/jOpt.%j.%N.out"
#SBATCH -p gpu
#SBATCH --gres=gpu:1
#SBATCH --nodes=1
#SBATCH --export=ALL
#SBATCH --ntasks-per-node=6
#SBATCH -t 48:00:00
export SLURM_NODEFILE=`generate_pbs_nodefile`
/home/crackauc/julia-a2f713dea5/bin/julia --machinefile $SLURM_NODEFILE /home/crackauc/projectCode/ImprovedSRK/Optimization/cometDriver.jl

Here I am only taking 6 nodes for the other computations, and I tell it to use the gpu node with -p and tell it I want only one GPU resource with –gres=gpu:1. If you want to use multiple GPUs, just change that number. However, you will want to split up the arrays amongst the multiple GPUs, change equalDiv to account for each CUDA core doing less calculations, send an integer to the GPU to tell it which GPU it is, and use that integer to change the indexing so that no calculations are repeated. That sounds like a good exercise.

The post Tutorial for Julia on the HPC with GPUs appeared first on Stochastic Lifestyle.

Multi-node Parallelism in Julia on an HPC (XSEDE Comet)

By: Christopher Rackauckas

Re-posted from: http://www.stochasticlifestyle.com/multi-node-parallelism-in-julia-on-an-hpc/

Today I am going to show you how to parallelize your Julia code over some standard HPC interfaces. First I will go through the steps of parallelizing a simple code, and then running it with single-node parallelism and multi-node parallelism. The compute resources I will be using are the XSEDE (SDSC) Comet computer (using Slurm) and UC Irvine’s HPC (using SGE) to show how to run the code in two of the main job schedulers. You can follow along with the Comet portion by applying and getting a trial allocation.

First we need code

The code I am going to use to demonstrate this is a simple parallel for loop. The problem can be explained as follows: given a 2-dimensional polynomial p(i,j) with coefficients c_{k}, find the area where |p(i,j)|<1. The function for generating these coefficients in my actual code is quite wild, so for your purposes you can replace my coefficients by generating a random array of 36 numbers. Also it's a semi-sparse polynomial of at most degree 8 for each variable, so create arrays of powers powz and powk. We solve for the area by making a fine grid of (i,j), evaluating the polynomial at each location, and summing up the places where its absolute value is less than 1.

I developed this "simple" code for calculating this on my development computer:

julia -p 4

Opens Julia with 4 processes (or you can use addprocs(4) in your code), and then

dx = 1/400
imin = -8
imax = 1
jmin = -3
jmax = 3
coefs,powz,poww = getCoefficients(A0,A1,B0,B1,α,β1,β2,β3,β4)
@time res = @sync @parallel (+) for i = imin:dx:imax
  tmp = 0
   for j=jmin:dx:jmax
    ans = 0
    @simd for k=1:36
      @inbounds ans += coefs[k]*(i^(powz[k]))*(j^(poww[k]))
    end
    tmp += abs(ans)<1
  end
  tmp
end
res = res*((imax-imin)*(jmax-jmin)/(length(imin:dx:imax)*length(jmin:dx:jmax)))
println(res)

All that we did was loop over the grid $i$ and the grid of $j$, sum the polynomial, check if its absolute value is less than 1, check how many times it is less than 1, and scale by the area we integrated. Some things to note is that I first wrote the code out the "obvious way" and then added the macros to see if they would help. @inbounds turns off array bounds checking. @simd adds vectorization at the "processor" level (i.e. AVX2 to make multiple computations happen at once). @parallel runs the array in parallel and @sync makes the code wait for all processes to finish their part of the computation before moving on from the loop.

Note that this is not the most efficient code. The problem is that we re-use a lot of floating point operations in order to calculate the powers of i and j, so it actually works out much better to unravel the loop:

@time res = @sync @parallel (+) for i = imin:dx:imax
  tmp = 0
  isq2 = i*i; isq3 = i*isq2; isq4 = isq2*isq2; isq5 = i*isq4
  isq6 = isq4*isq2; isq7 = i*isq6; isq8 = isq4*isq4
  @simd for j=jmin:dx:jmax
    jsq2 = j*j; jsq3= j*jsq2; jsq4 = jsq2*jsq2;
    jsq5 = j*jsq4; jsq6 = jsq2*jsq4; jsq7 = j*jsq6; jsq8 = jsq4*jsq4
    @inbounds tmp += abs(coefs[1]*(jsq2) + coefs[2]*(jsq3) + coefs[3]*(jsq4) + coefs[4]*(jsq5) + coefs[5]*jsq6 + coefs[6]*jsq7 + coefs[7]*jsq8 + coefs[8]*(i) + coefs[9]*(i)*(jsq2) + coefs[10]*i*jsq3
    + coefs[11]*(i)*(jsq4) + coefs[12]*i*jsq5 + coefs[13]*(i)*(jsq6) + coefs[14]*i*jsq7 + coefs[15]*(isq2) + coefs[16]*(isq2)*(jsq2) + coefs[17]*isq2*jsq3 + coefs[18]*(isq2)*(jsq4) +
    coefs[19]*isq2*jsq5 + coefs[20]*(isq2)*(jsq6) + coefs[21]*(isq3) + coefs[22]*(isq3)*(jsq2) + coefs[23]*isq3*jsq3 + coefs[24]*(isq3)*(jsq4) + coefs[25]*isq3*jsq5 +
    coefs[26]*(isq4) + coefs[27]*(isq4)*(jsq2) + coefs[28]*isq4*jsq3 + coefs[29]*(isq4)*(jsq4) + coefs[30]*(isq5) + coefs[31]*(isq5)*(jsq2) + coefs[32]*isq5*jsq3+ coefs[33]*(isq6) +
    coefs[34]*(isq6)*(jsq2) + coefs[35]*(isq7) + coefs[36]*(isq8))<1
  end
  tmp
end
res = res*((imax-imin)*(jmax-jmin)/(length(imin:dx:imax)*length(jmin:dx:jmax)))
println(res)

That's the fast version (for the powers I am using), and you can see how there simply are a lot less computations required by doing this. This gives almost a 10x speedup and is the fastest code I came up with. So now we're ready to put this on the HPC.

Setting up Comet

Log into Comet. I use the XSEDE single sign-on hub and gsissh into Comet from there. On Comet, you can download the generic 64-bit binary from here. You can also give compiling it a try yourself, it didn't work out to well for me and the generic binary worked fine. In order to do anything, you need to enter a compute node. To do this we open an interactive job with

srun -pty -p compute -t 01:00:00 -n24 /bin/bash -l

This gives you an interactive job with 24 cores (all on one node). Now we can actually compute things (if you tried before, you would have gotten an error). Now open up Julia by going to the appropriate directory and using

./julia -p 24

This will put you into an interactive session with 24 workers. Now install all your packages, etc., test your code, make sure everything is working.

Running Jobs

Now that Julia is all set up and you tested your code, you need to set up a job script. It's best explained via an example:

#!/bin/bash
#SBATCH -A <account>
#SBATCH --job-name="juliaTest"
#SBATCH --output="juliaTest.%j.%N.out"
#SBATCH --partition=compute
#SBATCH --nodes=8
#SBATCH --export=ALL
#SBATCH --ntasks-per-node=24
#SBATCH -t 01:00:00
export SLURM_NODEFILE=`generate_pbs_nodefile`
./julia --machinefile $SLURM_NODEFILE /home/crackauc/test.jl

In the first line you put the account name you were given when you signed up for Comet. This is the account whose time will be billed. Then you give your job a name and tell it where to save the output. Next is the partition that you wish to run on. Here I specify for it to be the compute node. Now I tell it the number of nodes. I wanted 8 nodes with 24 tasks per node. The time limit is 1 hour.

8 nodes? So we need to add some MPI code, right? NOPE! Julia does it for you! This is the amazing part. What we do is we export the Slurm node file and give it to Julia as the machinefile. This nodefile is simply a list of the compute nodes that are allocated to our job that is generated by the job manager. This will automatically open up one worker process for each thing in the node file (which will be 24 tasks per node, so there are 8*24= 192 lines in the node file and Julia will open up 192 processes) and run test.jl.

Did it work? A quick check is to have the following code in test.jl:

hosts = @parallel for i=1:192
       println(run(`hostname`))
       end

You should see it printout the names of 8 different hosts, each 24 times. This means our parallel loop automatically is on 192 cores!

Now add the code we made before to test.jl. When we run this in different settings, I get the following results: (SIMD is the first version, Full is the second "full unraveled" version)

8 Nodes:
SIMD - .74 seconds
Full - .324 seconds

4 Nodes:
SIMD - .77 seconds
Full - .21 seconds

2 Nodes:
SIMD - .81 seconds
Full - .21 seconds

1 Node
SIMD - .996 seconds
Full - .273 seconds

In this case we see that the optimal is to use 2 nodes. As you increase the domain you are integrating over / decrease dx, you have to perform more computations which makes using more nodes more profitable. You can check yourself that if you use some extreme values like 1/1600 it may be better to use 4-8 nodes. But this ends our quick tutorial into multi-node parallelism on Comet. You're done. If you have ever programmed with MPI before, this is just beautiful.

What about SGE?

Another popular job scheduler is SGE. They have this on my UC Irvine cluster. To use Julia with multi-nodes on this, you do pretty much the same thing. Here you have to tell it you want to do an MPI job. This will create the machine file and you stick that machine file into Julia. The job script is then as follows:

#!/bin/bash
 
#$ -N jbtest
#$ -q math
#$ -pe mpich 128
#$ -cwd            		# run the job out of the current directory
#$ -m beas
#$ -ckpt blcr
#$ -o output/
#$ -e output/
module load julia/0.4.3
julia --machinefile jbtest-pe_hostfile_mpich.$JOB_ID test.jl

That's it. SGE makes the machine file called jbtest-pe_hostfile_mpich.$JOB_ID which has the 128 processes to run (this is in the math queue, so for me it's split across 5 computers with the nodes repeated for the number of processes on that node), in your current directory, so I just load the Julia module and stick it into Julia as the machine file, test it out, and it prints out the name of compute nodes. On this computer I can even ssh into the nodes while a job is running to run htop. In htop I see that it uses as many cores on each computer that it says its using (sometimes a little bit more when it's using threading. You may need to set the number of BLAS threads to 0 if you are doing any linear algebra and don't want it to bleed). Success!

What about GPUs?

Using GPUs on this same problem is discussed in my next blog post!

The post Multi-node Parallelism in Julia on an HPC (XSEDE Comet) appeared first on Stochastic Lifestyle.